Магнитная гидродинамика, страница 18

Тогда в формуле (13.7.64) m=r, а К – есть натяжение на единицу площади, т,е. .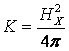

Поэтому скорость распространения поперечных колебаний проводящей жидкости в магнитном поле равна:

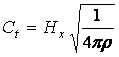 .                              (13.7.66)

В отличие от скорости распространения продольных колебаний, которая складывается из обычной скорости звука и скорости волн Альвена скорость распространения поперечных колебаний в невязкой жидкости с бесконечной проводимостью является единственной возможностью.

7.2 Уравнение Бернулли в магнитной гидродинамике.

Уравнение (13.7.60) представляет проекцию уравнения Навье-Стокса в магнитной гидродинамике на ось Х или линию тока, совпадающую с осью Х. Для стационарного движения из (13.7.60) имеем:

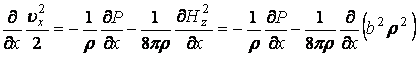 .         (13.7.67)

Поскольку ось Х совпадает с линией тока, то скорость жидкости имеет единственную компоненту u_{х ,} т.е. u_х²=u². по определению напряженность магнитного поля так же имеет единственную компоненту, перпендикулярную линии тока. Следовательно Н_z²=Н².

Правую часть уравнения (13.7.67) можно записать в виде:

 .

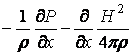В обычной термодинамике имеем:

 .

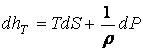В жидкости, лишенной трения и имеющей бесконечную проводимость энтропия каждого индивидуального объема постоянна, поэтому имеем:

 .

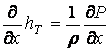Тогда уравнение (13.7.67) примет вид:

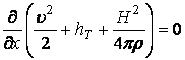
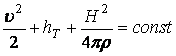                    . (13.7.68)

В (13.7.68) постоянная не зависит от Х, т.е. она постоянна для рассматриваемой линии тока. Уравнение (13.7.68) и есть уравнение Бернулли в магнитной гидродинамике.

Последнему уравнению можно придать иной вид, если в качестве давления взять полное давление P:

h=e_вн+ P V= .

Таким образом энтальпия в магнитной гидродинамике вследствие изменения внутренней энергии на величину  имеет вид:

 .

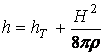Подставляя в уравнение Бернулли (13.7.68) имеем:

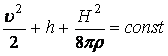 .                              (13.7.69)

Уравнение Бернулли в виде (13.7.69) представляет уравнение сохранения энергии частицы жидкости единичной массы вдоль линии тока.

8. Ударные  волны в магнитной гидродинамике

Для простоты рассмотрим прямую ударную волну в проводящей сжигаемой жидкости при отсутствии вязкости и при бесконечной проводимости. Рассмотрим лишь случай, когда напряженность магнитного поля направлена параллельно линии разрыва или перпендикулярно линии тока вещества.

На прямой ударной волне должны быть следующие величины:

-  плотность потока вещества:  .                                (13.8.70)

-  плотность потока импульса: 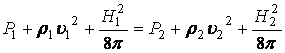        .(13.8.71)

-  плотность потока энергии: 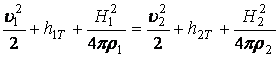 . (13.8.72)

Кроме того, в силу «вмороженности» магнитных силовых линий следует соотношение:

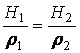        .                        (13.8.73)