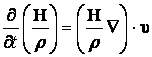Магнитная гидродинамика, страница 17

 .                                 (13.7.58)

Проектируя уравнения 1 (13.7.57) и      (13.7.58) получим:

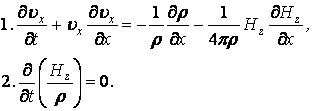                 (13.7.59)

Из второго уравнения системы (13.7.59) следует:

 ,   .

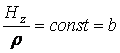Тогда первое уравнение системы (13.7.59) можно записать в виде:

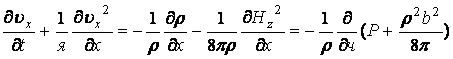 .      (13.7.60)

Из уравнения (13.7.60) не трудно видеть, что оно совсем не содержит магнитного поля и имеет обычный гидродинамический вид если в качестве давления взять давление определяемое соотношением:

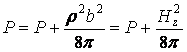 .                              (13.7.61)

Очевидно и все решения уравнения (13.7.60) можно получить из решений обычного гидродинамического уравнения если в них вместо Р подставить P. Этот результат почти очевиден, поскольку P  - представляет собой полное давление равное сумме гидростатического давления Р и магнитного давления .

В частности, скорость звука или скорость распределения малых возмущений вдоль оси Х представляющих из себя продольные волны сжатия может быть определена по известной формуле:

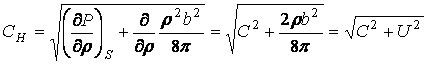 .      (13.7.62)

Из (13.7.62) следует, что скорость распространения малых возмущений в проводящей жидкости (s=¥) перпендикулярно магнитному полю возрастает на величину U равную:

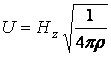 .                                (13.7.63)

Скорость U называется скоростью волн Альвена. Полученный результат физически понятен. Скорость распространения упругих продольных волн в проводящей жидкости в поперечном поле возрастает поскольку в силу натяжения магнитных силовых линий упругость проводящей среды как бы возрастает, что и ведет к к увеличению скорости.

Хотя ртуть имеет конечную проводимость (s¹¥) по формуле (13.7.63) можно оценить порядок скорости волн Альвена. При Н_Z=1000 э, r=13  имеем:

 .

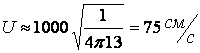Для скорости звука в ртути добавка очень мала, однако для разряженного вещества (ионосфера Земли, солнечная корона) скорость может оказаться сравнимой со скоростью звука. Очевидно на скорость распространения продольных колебаний направленных вдоль магнитного поля последнее не оказывает ни какого влияния.

Замечательно то, что в проводящей жидкости в магнитном поле могут распространяться и поперечные волны. Если первоначально возмущение перпендикулярно магнитным силовым линиям, то это возмущение распространяется вдоль силовой линии как по резиновому натянутому шнуру, что приведет (в силу «вмороженности» магнитных силовых линий) и распространению поперечных колебаний и материальной проводящей среде. Для вычисления скорости распространения колебаний распространения поперечных колебаний воспользуемся аналогией.

Уравнение поперечных колебаний в направлении оси Z струны расположенной вдоль оси X  как известно имеет вид:

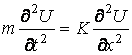 .                           (13.7.64)

Здесь U_Z  - смещение точек струны в направлении оси Z, m – масса струны на единицу длины,  K – натяжение струны. По общему свойству волнового уравнения   - есть скорость распространения волны вдоль оси x.

 .                                   (13.7.65)

Рассмотрим вещество, находящееся около магнитной силовой линии в прямоугольном параллелепипеде поперечным сечением (перпендикулярно силовой линии) равным 1 см².