Физически же пренебрежение токами смещения означает,
что между изменениями ![]() нет запаздывания. Значения
нет запаздывания. Значения
![]() в некоторый момент времени
определяется значениями
в некоторый момент времени
определяется значениями ![]() в тот же момент
времени. Таким образом, уравнения электродинамике в магнитной гидродинамике
имеют вид:
в тот же момент
времени. Таким образом, уравнения электродинамике в магнитной гидродинамике
имеют вид: 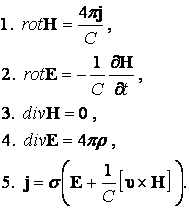 (13.1.6)
(13.1.6)
Из уравнений системы (13.1.6) следует, что уравнения движения проводящей жидкости и уравнения электродинамики могут быть связаны через силу Лоренца, входящую в закон Ома.
Уравнение движения проводящей жидкости в общем виде можно записать следующим образом:
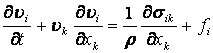 . (13.2.7)
. (13.2.7)
В
уравнении (13.2.7) ![]() -по-прежнему
массовая сила не электромагнитного происхождения. Для непроводящей жидкости,
как и прежде, имеем:
-по-прежнему
массовая сила не электромагнитного происхождения. Для непроводящей жидкости,
как и прежде, имеем:
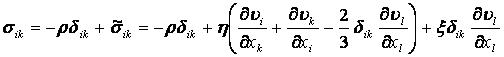 .
.
В проводящей же жидкости, находящейся в электрическом
и магнитном полях, возникают силы электромагнитного происхождения тензорного
характера. Эти силы определяются, как известно тензорами электрических и
магнитных напряжений. При постоянных ![]() они имеют вид:
они имеют вид:
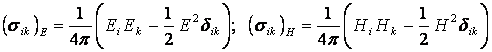 . (13.2.8)
. (13.2.8)
Силы электрического и магнитного происхождения, действующие на единицу массы проводящей жидкости, могут быть найдены по общему правилу:
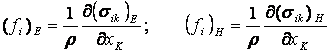 .
(13.2.9)
.
(13.2.9)
Очевидно, следует добавить к правой части уравнения (13.2.7).
Найдем силу, действующую на единицу массы со стороны
электрического поля (![]() ):
):

Не трудно видеть, что последнее выражение можно записать в следующем векторном виде:
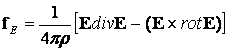 .
.
Если на вещество действует только электрическое поле,
то из системы уравнений (13.1.6) следует (при ![]() ),
что
),
что ![]() . Принимая во внимание систему (13.1.6) имеем:
. Принимая во внимание систему (13.1.6) имеем:
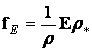 . (13.2.10)
. (13.2.10)
Рассмотрим силы, действующие на проводящее вещество в магнитном поле. Если выделить в веществе единичный кубик с гранями, перпендикулярными осям координат (рис.1), то силы, действующие на грани этого кубика можно получить, рассмотрев компоненты тензора магнитных напряжений:
 . (13.2.11)
. (13.2.11)
 |
Так, силы, действующие нормально к граням кубика, очевидно, представляют из себя магнитные давления и равны:
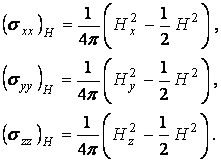
Недиагональные элементы тензора напряжений, очевидно, представляют собой касательные силы, действующие на грани единичного кубика:
 (13.2.12)
(13.2.12)
Пусть постоянное магнитное поле направлено вдоль оси ![]() то есть
то есть ![]() .Представим
себе, что элементарные кубики нанизаны на соседние магнитные силовые линии.
Тогда взаимодействие магнитного поля с веществом можно в духе Максвелла
представить в виде отталкивания друг от друга магнитных силовых линий с силой
.Представим
себе, что элементарные кубики нанизаны на соседние магнитные силовые линии.
Тогда взаимодействие магнитного поля с веществом можно в духе Максвелла
представить в виде отталкивания друг от друга магнитных силовых линий с силой 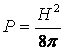 и их натяжения с силой
и их натяжения с силой 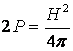 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.