Сама величина этого стационарного (в турбулентном смысле) поля может быть определена лишь из решения уравнений (13.6.54) и (13.6.55).
Однако, очевидно можно сделать следующее заключение. Если ![]() , то диссипация магнитного поля через
индукционные токи (
, то диссипация магнитного поля через
индукционные токи (![]() ) будет меньше и магнитное
поле может возрастать даже благодаря растяжению магнитных силовых линий.
) будет меньше и магнитное
поле может возрастать даже благодаря растяжению магнитных силовых линий.
Если же ![]() , то напряженность
магнитного поля должна убывать.
, то напряженность
магнитного поля должна убывать.
Таким образом, для того, чтобы напряженность спонтанного магнитного поля при турбулентном движении проводящей жидкости возрастала необходимо, чтобы выполнялось условие:
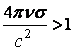 . (13.6.56)
. (13.6.56)
Возрастание напряженности магнитного поля не может быть беспредельной, т.к. сильное магнитное поле в свою очередь будет подавлять механическое турбулентное движение, и наше рассмотрение будет несправедливым. Поскольку в уравнении Навье-Стокса уже нельзя будет пренебрегать магнитной массовой силой.
Из общих физических соображений ясно, что максимальная напряженность магнитного поля не должна превышать величину при которой энергия единицы объема магнитного поля примерно равна кинетической энергии единицы объема движущейся жидкости.
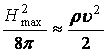 .
.
Рассмотренный механизм позволяет объяснить возникновение значительных магнитных полей во вселенной и в частности на Солнце.
К сожалению проверить сделанные выше выводы в земных условиях довольно
затруднительно, т.к. например для ртути (s=1016 ![]() , n=10-7
, n=10-7 ![]() ) имеем:
) имеем:
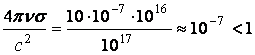 .
.
Однако во вселенной в достаточно разреженных (малая плотность) ионизированных (большая проводимость) газовых скоплениях условие (13.6.56) может выполняться, и в этом случае в газовых скоплениях и на поверхности Солнца могут существовать значительные магнитные поля напряженностью в десятки и сотни эрстед.
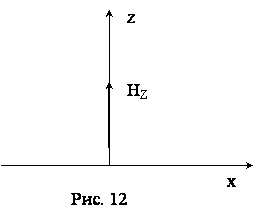 Рассмотрим
одномерное движение проводящей сжимаемой жидкости в поперечном магнитном поле
(рис.12 ). Пусть ось Х направлена вдоль линии тока, а ось Z
перпендикулярно к ней. Пусть напряженность магнитного поля имеет единственную
компоненту перпендикулярную линии тока и, следовательно, оси Х. Таким
образом, топология движения определена следующим образом:
Рассмотрим
одномерное движение проводящей сжимаемой жидкости в поперечном магнитном поле
(рис.12 ). Пусть ось Х направлена вдоль линии тока, а ось Z
перпендикулярно к ней. Пусть напряженность магнитного поля имеет единственную
компоненту перпендикулярную линии тока и, следовательно, оси Х. Таким
образом, топология движения определена следующим образом:
uz=0 , ux=ux(x) , uy=0 ,
Hx=0 , Hy=0 , Hz=Hz(x)
Будем полагать, что жидкость имеет бесконечную проводимость s=¥ и является идеальной в гидродинамическом смысле (h=x=0). В такой жидкости не может происходить никаких диссипативных процессов ни вследствие вязкости жидкости ни вследствие джоулевых потерь (S=const).
Уравнения движения такой жидкости имеет вид:
1.
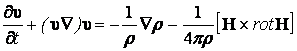 ,
,
2.
![]() , (13.7.57)
, (13.7.57)
3.
![]() .
.
Как было показано выше из уравнений 2, 3 системы (13.7.57) следует:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.