Магнитная гидродинамика, страница 5

Решения системы должны удовлетворять дополнительным условиям:

 ,    .                               (13.2.17)

13.2.3. Граничные условия

Запишем наиболее характерные граничные условия.

1.На неподвижной твердой поверхности . Если тело движется в жидкости со скоростью , то в каждой точке поверхности тела должно выполняться условие: .

2. На границе двух несмешивающихся проводящих жидкостей:

 ,       ,            .

В последнем выражении  - плотность поверхностного тока на границе жидкостей.

Из 4 и 5 уравнений системы          (13.2.16) можно исключить напряженность электрического поля . Для этого возьмем операцию  от обеих частей уравнения 4 системы     (13.2.16):

,

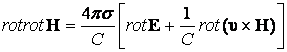поскольку .Получаем:

 .

Последнее соотношение, так как  можно записать в следующем виде:  

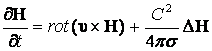 .                     (13.2.18)

Если не интересоваться напряженностью электрического поля, то тогда полная система уравнений будет состоять из уравнений 1, 2, 3 системы   (13.2.16)и уравнения(13.2.18). В этом случае будем иметь лишь 8 уравнений с 13 неизвестными. Если из этой системы найдена напряженность магнитного поля, как функция координат и времени, то напряженность электрического поля при необходимости может быть найдена из уравнения 5 системы (13.2.16).

Для несжимаемой жидкости уравнения системы (13.2.16) упрощаются.

Для несжимаемой жидкости имеем:

 ,       .

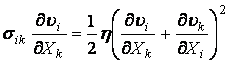В частности уравнение движения примет вид:

 .

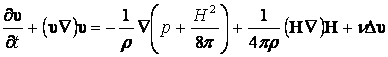Здесь использована векторная формула:

 .

13.2.4 Тензор плотности потока импульса

Тензор плотности потока импульса, очевидно, имеет вид:

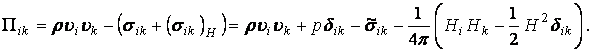                                                                                                                     (13.2.19)

Здесь  - тензор вязких напряжений в обычной гидродинамике. Здесь опущен тензор электрических напряжений , как указывалось выше, в проводящей жидкости не может быть сколько-нибудь значительных электрических полей.

13.2.5. Вектор Умова

Вектор плотности потока энергии – вектор Умова в обычной гидродинамике имеет вид:

 .                           (13.2.20)

В выражении (13.2.20)  - полная энергия единицы массы жидкости,  - плотность потока тепла,  - тензор напряжений. В магнитной гидродинамике к указанным в (13.2.20) членам следует добавить плотность потока электромагнитной энергии – вектор Пойтинга: