Магнитная гидродинамика, страница 15

Однако существует возможность увеличить скорость отбрасываемого вещества экспериментальными способами.  Это можно сделать в устройстве типа электромагнитного насоса прямого действия если газ является достаточно хорошо проводящей плазмой. Если же в двигателе каким-либо способом организовать источник ионов, то их можно разогнать то их можно разогнать в электростатическом поле практически до субсветовых скоростей. Конечно как в том, так и в другом случае на борту космического корабля должен быть достаточно мощный источник электрической энергии.

6. Спонтанное магнитное поле при турбулентном движении проводящей жидкости

Из принципа ”вмороженности” магнитных силовых линий в вещество следует, что магнитное поле будет препятствовать возникновению турбулентного режима течения проводящей жидкости. Так если поле направлено вдоль трубы по которой течет проводящая жидкость то очевидно что возникновение поперечных составляющих скорости вследствие натяжения при этом магнитных силовых линий будет затруднено, а следовательно переход от ламинарного режима течения к турбулентному будет происходить при больших числах Рейнольдса  нежели в непроводящей жидкости или в проводящей жидкости, но без магнитного поля. Точно также магнитное поле направленное вдоль танцевального разрыва в проводящей жидкости увеличивает его устойчивость.

Турбулентное движение проводящей жидкости обладает интересным свойством, свойством возникновения в нем сравнительно больших магнитных полей.

В проводящей жидкости всегда существуют эффекты приводящие к возникновению слабых магнитных полей, например магнитомеханический эффект или флуктуации электрического заряда.

Рассмотрим, как будет вести себя в дальнейшем раз возникшее слабое магнитное поле при турбулентном движении проводящей жидкости.

Для этого, очевидно, мы должны рассмотреть два конкурирующих эффекта.

При движении жидкости в возникшем слабом магнитном поле в ней будут наводиться индукционные токи, а следовательно будет происходить диссипация электрической энергии из-за джоулевых потерь, что в конечном счете должно уменьшать спонтанно возникшее магнитное поле.

С другой стороны поле будет стремиться увеличиться в силу принципа ”вмороженности” магнитных силовых линий поскольку оно пропорционально расстоянию между двумя близкими жидкими частицами, а это расстояние при турбулентном движении в среднем всегда увеличивается с течением времени.

Очевидно, что при некоторых условиях обе тенденции могут оказаться равносильными и в турбулентной жидкости возникнет магнитное поле определенной напряженности.

Для оценки этой напряженности рассмотрим уравнения движения.

До тех пор пока напряженность магнитного поля мала в уравнении движения Навье-Стокса для несжимаемой жидкости можно пренебречь магнитной массовой силой как квадратичной по малой величине Н. Тогда уравнение Навье-Стокса можно, как указывалось выше записать в следующем виде:

                             ,  .                            (13.6.54)

В магнитной гидродинамике для напряженности магнитного поля имеем следующее уравнение:

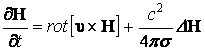                                      .                       (13.6.55)

Сравнивая уравнения           (13.6.54) и (13.6.55) обнаруживаем, что эти уравнения совершенно идентичны, а если , то и тождественны при этой замене  и .

Следовательно, должны учитывать решения этих уравнений вида:

                                               =const .

В этом случае при постоянной завихренности может присутствовать и стационарное магнитное поле. При этом ни завихренность ни магнитное поле не увеличиваются и не убывают.