Магнитная гидродинамика, страница 4

В однородном магнитном поле эти силы, действующие на соседние элементы объема, взаимно компенсируются и не приводят к их взаимному перемещению. Не скомпенсированные силы, приводящие к движению вещества, возникают только тогда, когда существуют градиенты магнитного поля и определяются по общему правилу:

 .

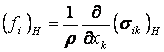Здесь, -ая компонента силы, действующей со стороны магнитного поля на единицу массы вещества. Таким образом, если пользоваться наглядным представлением об отталкивании магнитных силовых линий и их натяжении,  то можно сказать, что магнитные силовые линии всегда стремятся выпрямиться или сжаться (если они замкнутые) вследствие их натяжения, а их распределение в веществе стремится стать однородным вследствие их взаимного отталкивания.

Таким образом, сила, действующая на единицу массы проводящей жидкости со стороны магнитного поля,  равна ():

 .

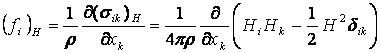По аналогии с предыдущим вычислением имеем:

 .

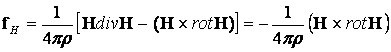Согласно уравнениям Максвелла (13.1.6) получаем:

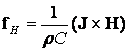 .                                               (13.2.13)

Таким образом, в уравнении движение Навье Стокса должен быть добавлен еще один член (13.2.13), представляющий собой массовую силу, действующую со стороны магнитного поля на движущуюся  проводящую жидкость.

Рассмотрим остальные уравнения полной системы уравнений движения вязкой проводящей жидкости.

Очевидно, что уравнение непрерывности, как уравнение сохранения вещества полностью сохранит свой вид:

 .                                        (13.2.14)

Обратимся к уравнению сохранения внутренней энергии, для непроводящей жидкости имели:

  ,    .

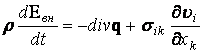Из последнего уравнения следует, что внутренняя энергия единицы объема непроводящей жидкости изменяется вследствие притока тепла извне в эту единицу объема, а также вследствие его сжатия и диссипации в нем механической энергии из-за вязкости жидкости.

В проводящей жидкости появляется еще один источник изменения внутренней энергии единицы объема жидкости - это джоулевы потери. Джоулевы потери в единице объема проводящей жидкости равны:

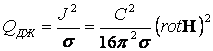 .                     (13.2.15)

С учетом (13.2.13) и (13.2.15) уравнения движения проводящей жидкости в магнитном поле имеют вид:

1.  ,

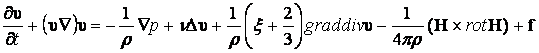2.  ,

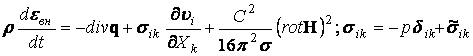3. ,                                                                          (13.2.16)

4.  ,

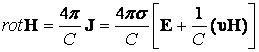5.  .                                                             

В уравнении 1 системы         (13.2.16) - массовая сила не электромагнитного происхождения, например сила тяжести. В 2 системы      (13.2.16)  - тензор напряжений не проводящей жидкости определяемый соотношениями (13.2.7). Система          (13.2.16) содержит 11 уравнений для нахождения 16 неизвестных . Вместе с калорическим уравнением состояния  и термическим уравнением состояния  система        (13.2.16) полностью определяет механические термодинамические характеристики проводящей жидкости движущейся в магнитном поле. Для ее решения необходимо задать четыре феноменологических коэффициента - ,  - коэффициенты вязкости,  - коэффициент теплопроводности и  - проводимость жидкости.