Магнитная гидродинамика, страница 7

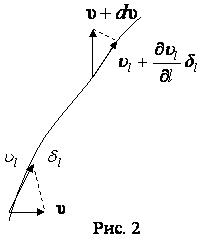
Рассмотрим малый участок этой жидкости. Так как скорости концов участка  жидкой линии различны, то она будет растягиваться или сжиматься, Найдем изменение длины выделенного участка  с течением времени, Очевидно, что за время  участок  получит приращение:

. Последнее соотношение можно записать в следующем виде:

 .

Здесь  - единичный вектор отрезка . Можно далее записать:

 ,               .

Или в векторном виде предыдущее выражение можно записать:

 ,                .        (13.3.29)

Сравнивая уравнения (13.3.29) и (13.3.28) приходим к заключению, что величины  и  описываются одним и тем же уравнением. Если при этом начальные и граничные условия к обоим уравнениям идентичны, то и решения  будут тождественны.

Отсюда можно сделать следующие заключения:

1.  Если в некоторый начальный момент времени вектора   и  были параллельны, то они останутся параллельными и во все последующие моменты времени, а их величины будут изменяться пропорционально. Это в свою очередь означает, что если две близкие жидкие частицы находились на одной магнитной линии, то они останутся на ней во все последующие моменты времени.

2.  Если расстояние между двумя жидкими частицами увеличивается, то соответственно увеличивается и  величина .

Таким образом, если перейти к конечным расстояниям между жидкими частицами, то можно прийти к выводу, что, если вещество с бесконечной проводимостью перемещается  в магнитном поле, то вместе с ним перемещается и магнитное поле. Обзорно говоря, магнитные силовые линии как бы «вклеены», «вморожены» в вещество. Если , то вследствие растяжения жидкой линии напряженность магнитного поля вдоль нее будет увеличиваться и наоборот.

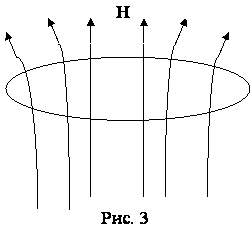
Рассмотрим некоторый жидкий контур (рис. 3) перпендикулярный напряженности магнитного поля. Если теперь каким-либо образом стянуть этот контур, то в силу вмороженности магнитных силовых линий стянется и магнитное поле. Поскольку поток напряженности магнитного поля через этот контур останется постоянным, то при сокращении контура напряженность поля внутри его увеличивается, это явление используется при создании сверхсильных импульсных магнитных полей. Вещество сжимается взрывом, в результате чего магнитное поле на короткое время в некоторой ограниченной области достигает сотен тысяч эрстед.

 

На этом же принципе основано устройство сверхпроводящих экранов. Если есть необходимость какую-то часть экспериментального объема защитить от воздействия внешних магнитных полей, то она окружается оболочкой из сверхпроводника, охлаждаемого жидким гелием. И в этом случае магнитные силовые линии внешних магнитных полей «приклеенные» к сверхпроводящей оболочке не могут проникнуть внутрь экспериментального объема.