Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 9

   Эффективную ширину спектра случайного процесса можно определить и другими способами, например исходя из условия уменьшения значений спектра мощности на границе этого частотного интервала до уровня 0.1 W_тах.. Эффективная ширина спектра  тесно связана с понятием интервала корреляции. Этот интервал служит количественной характеристикой, служащей для оценки "скорости изменения" случайного процесса, он определяется как

                                            

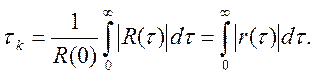
   Интервал корреляции может быть оценен и через эффективную ширину спектра по теореме Винера – Хинчина.  В любом случае произведение

                                             

это следует из свойств преобразования Фурье, оно называется соотношением неопределенности.

   Для иллюстрации введенных понятий на Рис.4.1 в центре приведены примеры реализаций двух случайных процессов, слева — автокорреляционные функции этих процессов, а справа — их спектры плотности мощности.

 

       Рис.4.1. Взаимосвязь (на качественном уровне) между видом реализаций случайных процессов (б), их корреляционными функциями (а) и спектрами мощности (в).

   Белый шум. Так называют стационарный случайный процесс, спектральная плотность мощности которого постоянна на всех частотах:

                                                  

   Согласно теореме Винера – Хинчина корреляционная функция белого шума представляет собой дельта-функцию:

                                                 

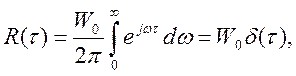
т.е. она равна нулю всюду, кроме точки t =0. Дисперсия белого шума бесконечно велика.

   В несовпадающие моменты времени значения белого шума некоррелированы — как бы ни был мал интервал  t, сигнал за это время может измениться на любую величину.

   Белый шум является абстрактной математической моделью и физически существовать не может. Это объясняется прежде всего бесконечностью его дисперсии (т. е. средней мощности). Однако в тех случаях, когда полоса пропускания исследуемой цепи существенно уже эффективной ширины спектра шума, который на нее воздействует, можно для упрощения анализа приближенно заменить реальный случайный процесс

 белым шумом.

   Замечание Отметим еще раз, что вероятностные и корреляционные (или спектральные) характеристики случайного процесса – это совершенно различные и не связанные между собой функции. Так, например, нормальный случайный процесс может иметь самую разнообразную спектральную плотность мощности, а белый шум – произвольную функцию распределения. Единственная «точка соприкосновения» вероятностных и корреляционных характеристик — это возможность расчета дисперсии случайного процесса как на основе одномерной плотности вероятности, так и исходя из корреляционной функции при =0.

   Узкополосные случайные процессы. Важную роль на практике играет особый класс случайных процессов, спектр которых сосредоточен в относительно малой полосе частот, сосредоточенных вблизи некоторой средней частоты . Схематически это показано на Рис. 4.2

 

Рис.4.2 Узкополосный случайный процесс

   Узкополосный характер спектра говорит о том, что сам сигнал имеет вид квазигармонического колебания :

                                                 )                                 (4.7)

   Огибающая этого процесса и начальная фаза являются случайными медленно меняющимися функциями времени (в масштабе  )   

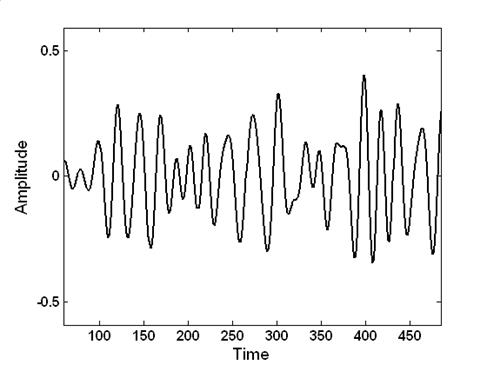
                                              Рис.4.3. Узкополосный случайный процесс

   Осциллограмма такого процесса показана на Рис.4.3, видим, что он  действительно является квазигармоническим.

Примечание:Выше мы выяснили, что для гармонических сигналов корреляционная   функция является тоже гармонической. Поскольку сигнал (4.7) является квазигармоническим, то его  корреляционная функция  будет тоже квазигармонической.