Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 5

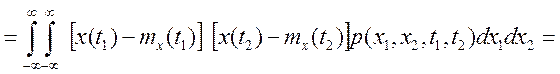
                                                      (2.7)

   Корреляционная функция характеризует степень статистической связи тех значений случайного процесса, которые наблюдаются при  изменении промежутка времени t_2. -  t_1.   При  t_2. =  t₁  последнее выражение соответствует определению дисперсии случайного процесса X(t). Следовательно, при совмещении сечений функция корреляции равна дисперсии:

                                                             (2.8)

Пример 1. Рассчитаем корреляционную функцию гармонического сигнала со случайной   начальной фазой:

 Этот сигнал схематически показан на Рис.2.1.

 

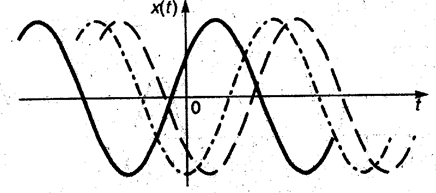Рис.2.1. Гармонический сигнал со случайной фазой.

  Начальная фаза φ в большинстве практически интересных случаев может считаться равномерно распределённой на интервале 0…2π. Таким образом, Рис.2.1 отражает ряд синусоид, смещённых по оси времени случайным образом.

Очевидно, что данный случайный процесс является центрированным, т. е. его математическое ожидание не зависит от времени и равно нулю:

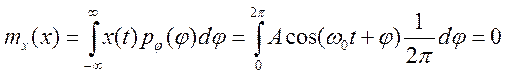                           (2.9)

Поэтому ковариационная и корреляционная функции данного процесса совпадают и могут быть найдены следующим образом (поскольку реализации данного случайного процесса представляют собой функции, зависящие от одной случайной величины, для усреднения произведения нет нужды прибегать к двумерной плотности вероятности — достаточно воспользоваться формулой (2.9), позволяющей произвести усреднение произвольной функции от случайной величины):

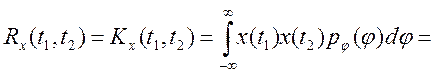
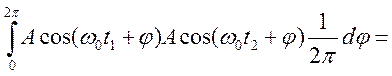
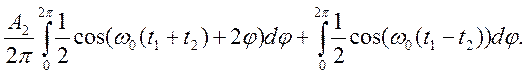
Здесь в первом слагаемом интегрирование проводится по двум периодам функций соs поэтому данный интеграл равен нулю. Во втором слагаемом подынтегральная функция не зависит от переменной интегрирования φ, так что результат интегрирования равен произведению подынтегрального выражения и длины промежутка интегрирования, равной 2π. Окончательно получаем

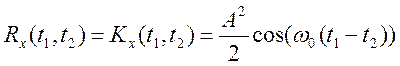                      (2.10)

Как видим, корреляционная функция данного случайного процесса гармонически зависит от расстояния между анализируемыми моментами времени. При совпадении моментов времени      получаем величину дисперсии случайного процесса:

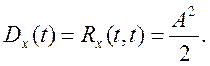                                    (2.11)

   Данный результат очевиден: мощность гармонического  сигнала равна половине квадрата его амплитуды.

Некоррелированность и статистическая независимость.

    Если совместно рассматривать две случайные величины Х1 и Х2  между ними может существовать либо не существовать статистическая связь. Отсутствие такой связи означает, что плотность вероятности одной случайной величины  не зависит от того, какое значение принимает другая случайная величина. Двумерная плотность вероятности при этом представляет собой произведение одномерных плотностей:

   Это условие называется условием статистической независимости.

   При наличии статистической связи между случайными величинами статистические свойства каждой из них зависят от значения, принимаемого другой случайной величиной. Эта связь может быть сильной или слабой, линейной или нелинейной. Мерой линейной статистической связи между случайными величинами является коэффициент корреляции:

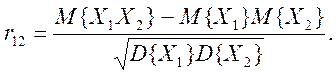                       (2.12)

    Можно показать, что   

    Предельные значения ±1 достигаются, если реализации случайных величин жестко связаны линейным соотношением  где а и b  —  некоторые константы. Знак коэффициента корреляции при этом совпадает со знаком множителя а.

Равенство коэффициента корреляции нулю свидетельствует об отсутствии линейной статистической связи между случайными величинами (при этом говорят об их некоррелированности). Как видно из (2.12), при этом математическое ожидание произведения случайных величин равно произведению их математических ожиданий.

   Легко показать, что из статистической независимости следует некоррелированность случайных величин. Обратное утверждение в общем случае неверно — некоррелированные случайные величины могут быть зависимыми  (это может обнаружиться при анализе их моментных функций более высоких порядков) [ 3 ].