Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 4

Так как  модуль (1.15) равен единице, то интеграл   (1.16) сходится при любых вещественных значениях   для всех функций распределения  .

    Самое важное свойство характеристических функций:

характеристическая функция суммы случайных величин равна произведению характеристических функций слагаемых.

   Это обстоятельство широко используется при теоретическом анализе комбинаций случайных процессов. Доказательство этого можно найти, например,  в [ 3 ].

     Далее, при анализе случайных процессов часто используются понятия кумулянтов или семиинвариантов k-го порядка случайной величины. Они представляют собой производную k-го порядка логарифма характеристической функции в точке , умноженную на  . С их помощью часто удается облегчить процедуру нахождения моментных функций случайных величин.

Раздел 2. КОРРЕЛЯЦИОННЫЕ ФУНКЦИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

Одномерная плотность вероятности и связанные ней числовые характеристики позволяют получить важную информацию о свойствах случайного процесса, из которого взято одномерное сечение. Однако, как правило,  для исследования реальных случайных процессов таких сведений недостаточно, поскольку они дают вероятностное представление о случайном процессе X(t) только в отдельные моменты времени и ничего не говорят о том, как он изменяется во времени. Гораздо больше сведений можно получить, располагая двумя сечениями случайного процесса в произвольные моменты времени  и   . Это образует двумерную случайную величину, которая описывается двумерной плотностью вероятности :

                                       

Это произведение  представляет собой  вероятность того, что реализация случайного процесса X(t) в момент времени t₁попадает в бесконечно малый интервал шириной    в окрестности , а в момент времени t₂ — в бесконечно малый интервал шириной в окрестности

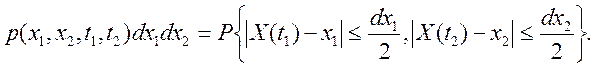                                      (2.1)

   Естественным обобщением является n-мерное сечение случайного процесса, приводящее к  n-мерной плотности вероятности

                                                                                                (2.2)

 По аналогии с одномерным случаем вводится многомерная интегральная функция распределения

                                                                                                (2.3)

определяющая вероятность того, что значения случайного процесса X(t) во все моменты времени не превосходят  :

                                                                                   (2.4)

Описание свойств случайных процессов с помощью многомерных плотностей вероятности высокой размерности дает весьма подробные сведения, однако на этом пути часто встречаются серьезные математические трудности, К счастью, многие задачи, связанные с описанием случайных сигналов, удается решить на основе двумерной плотности вероятности .

 В частности, задание двумерной плотности вероятности  позволяет определить важную характеристику случайного процесса — его ковариационную функцию:

                                                                                     (2.5)

Согласно этому определению, ковариационная функция случайного процесса X(t) представляет собой статистически усредненное произведение значений случайной функции X(t) в моменты времени     и   .

Для каждой реализации случайного процесса произведение является некоторым числом. Совокупность реализаций образует множество случайных чисел, распределение которых характеризуется двумерной плотностью вероятности .  Если эта плотность вероятности известна, операция усреднения по множеству осуществляется по формуле

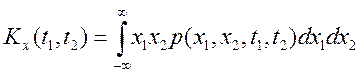                                                                             (2.6)

   Часто при анализе случайных процессов основной интерес представляет их флуктуационная составляющая. В таких случаях применяется корреляционная функция, представляющая собой статистически усредненное произведение значений центрированной случайной функции         в моменты времени     и   _.: