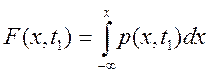Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 3

(1.7)

   Математическое ожидание и дисперсия. Знание одномерной плотности вероятности позволяет провести операцию статистического усреднения как самой случайной величины, так и любой функции от неё. Под статистическим усреднением   подразумевается    усреднение по множеству (по ансамблю реализаций) в данном сечении процесса, т. е. в фиксированный момент времени . Наибольшее значение имеют следующие параметры случайного процесса:

·  математическое ожидание, которое служит  теоретической оценкой среднего  значения случайного процесса в момент времени :

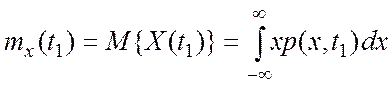                                                                (1.8)

Замечание 1.

Во многих практических задачах приходится вычислять математическое ожидание некоторой функции от случайной величины х, имеющей плотность вероятности р(х). Такое вычисление выполняется по формуле:

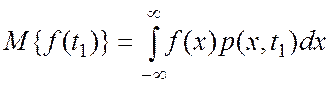                               (1.9)

Заметим, что формула для математического ожидания (1.9) является частным  случаем (1.8).

·  дисперсия, характеризующая среднюю мощность отклонений случайного процесса от 

его среднего значения      Эти отклонения часто называют флуктуациями.     Обозначение дисперсии:

  

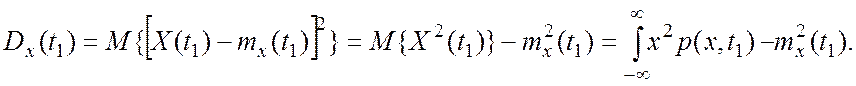
                                                                                                                                              (1.10)

   Дисперсия случайной величины часто обозначается как        .

·  среднее квадратическое отклонение, представляющее собой квадратный корень из дисперсии и служащее амплитудной мерой разброса значений случайного процесса  относительно математического ожидания:

                                                                        (1.11)

·  мода распределения случайной величины представляет собой наивероятнейшее значение случайного процесса в момент времени , т.е. значение, при котором достигается максимум плотности вероятности.

·  медиана распределения случайной величины представляет собой такое значение случайного процесса в момент времениt , отклонения от которого в любую сторону равновероятны. Математически это можно записать таким образом:

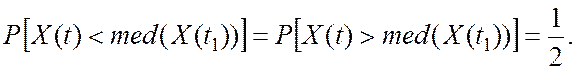                                   (1.12)

Моментные функции случайных величин

 Математическое ожидание и дисперсия – это примеры так называемы моментных функций (первого и второго порядков). Кроме них часто употребляются моментные функции более высоких порядков, в общем случае  моментные функции k-го порядка:

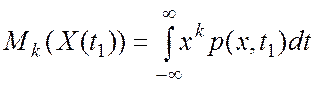                                                                                   (1.13)

В практике статистического анализа моментные функции выше четвертого порядка употребляются редко. Это связано с быстрым нарастанием статистических погрешностей их оценок при увеличении k. Этот вопрос рассматривается в специальных руководствах по математической статистике, например, в [ 8 ].

Зато комбинации моментных функций до четвертого порядка широко используются. В частности,

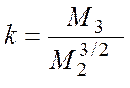                             носит название коэффициента асимметрии ,

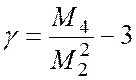                              коэффициента эксцесса                                         (1.14)

Эти коэффициенты служат для оценки отличий плотности вероятности от нормального (гауссова) закона. В зарубежной литературе коэффициент эксцесса часто не содержит вычитаемой тройки.

Характеристическая функция случайной величины.

Формула (1.9) дает общий вид математического ожидания любого функционального преобразования  случайной величины. В математических приложениях важное значение имеет специальный вид такого преобразования, а именно

                                                                                (1.15)

где V – произвольный вещественный параметр. Среднее значение величины  называется   характеристической функцией  случайной величины X(t₁) или характеристической функцией данного распределения вероятностей .По определению,

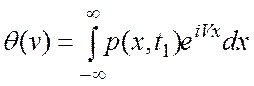                                                                                  (1.16)