Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 2

   Работа имеет также экспериментальную часть, где аналоговые случайные процессы преобразуются в различных линейных и нелинейных цепях, затем преобразуются в цифровые реализации, записываются в память ЭВМ и затем обрабатываются. Эта часть работы содержит важный инновационный элемент – применение современных аналого-цифровых преобразователей на базе быстродействующих микропроцессоров цифровой обработки сигналов семейства ADSP–2100. Вся расчетная часть работы, а также обработка результатов экспериментов выполняется на базе математического пакета МАТЛАБ и его расширений –  Data Acquisition и Statistical Toolbox. Используются заложенные в них возможности математического моделирования разнообразных типов сигналов, а также развитые средства компьютерной графики.

Материал данного описания содержит необходимые первоначальные сведения по теории случайных процессов, обзор методов  статистического описания их параметров  и практическую часть – моделирование сигналов с различными функциями распределения вероятности и получение экспериментальных реализаций сигналов на лабораторной установке. Обработка их дает оценки параметров конкретных случайных процессов.

Раздел 1. КРАТКИЕ СВЕДЕНИЯ ПО ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ

   Ансамбль реализаций. Обычно рассмотрение теории случайных процессов начинается с введения понятия  ансамбля реализаций. Такой ансамбль показан на Рис.1.1, считается, что  все его отдельные реализации подчиняются одним и тем же статистическим закономерностям.

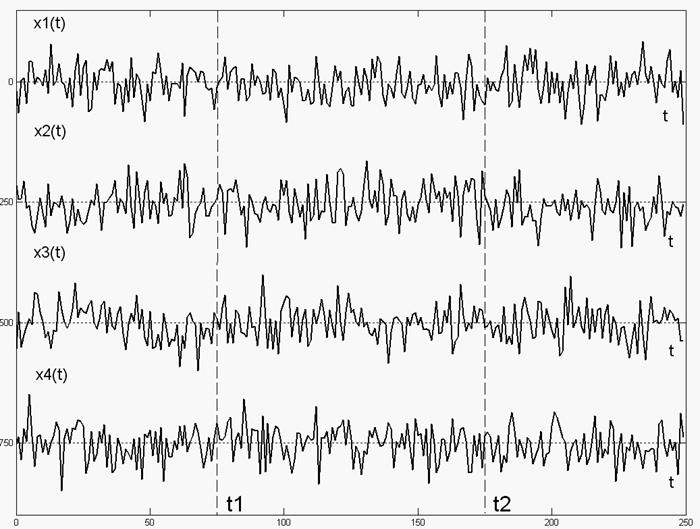
   Рис.1.1.Ансамбль реализаций случайного процесса

Рис.1.1 Ансамбль реализаций случайного процесса

На Рис.1.1 показан ансамбль из четырех реализаций. Будем считать, что таких реализаций , причем .

 Пусть Х(t) — случайный процесс, заданный ансамблем реализаций  Выбрав произвольный момент времени , зафиксируем значения, принимаемые всеми реализациями ,  (см. рис. 1.1). Совокупность этих значений (при большом количестве реализаций) образует одномерное сечение случайного процесса и представляет собой случайную величину . Рассмотрим кратко основные характеристики одномерных случайных величин, образуемых при одномерном сечении.

 Интегральная функция распределения вероятности  равна вероятности того, что в момент времени  значение случайного процесса не превосходит x:

              (1.1)

   Функция F(х, ) является неубывающей, её значения лежат в диапазоне .

Для предельных значений х выполняются следующие соотношения:    

                                                                          (1.2)

Одномерная плотность вероятности представляет собой производную от функции распределения:

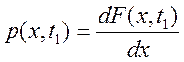                                                                                 (1.3)

  Произведение  представляет собой   вероятность  попадания значения случайного процесса Х(t₁) в бесконечно малый интервал шириной     в окрестности  :

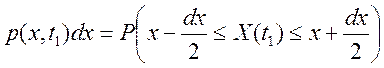                                                                                                                                                                                       (1.4)

  откуда следует, что плотность вероятности является неотрицательной функцией:

                                                         

    Чтобы рассчитать вероятность попадания значения в произвольный интервал [a ,b], необходимо вычислить следующий интеграл:

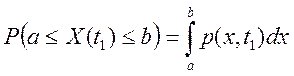                                                                                            (1.5)                 

   Так как случайная величина обязательно принимает какое-нибудь значение, должно выполняться условие нормировки:

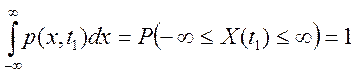                                                                                                                                                                                                                                                     (1.6)

      Зная плотность вероятности, можно рассчитать интегральную функцию распределения: