Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 12

 

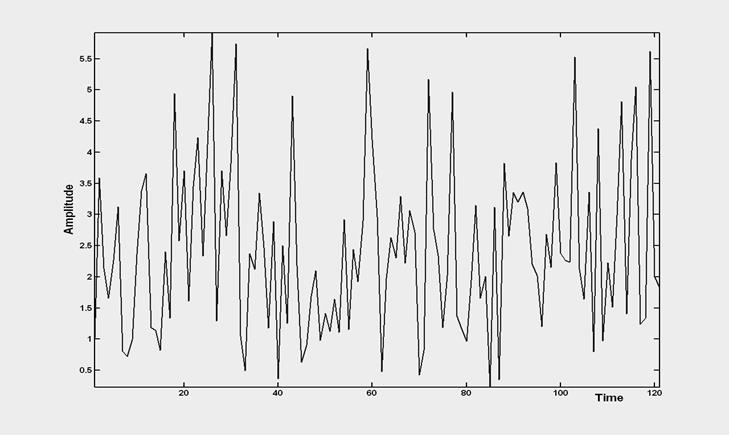
                      Рис.5.3. Участок реализации релеевского процесса

Как видно из Рис.5.3, реализация релеевского процесса содержит характерные положительные выбросы амплитуды, что соответствует верхнему "хвосту" гистограммы Рис.5.2.

Задание 5.2. Постройте гистограммы упомянутых    выше   трех распределений для разных значений дисперсии процессов и  объема выборки, проведите  сравнительный анализ их параметров

.

   Построение гистограмм можно выполнить также непосредственно из МАТЛАБ, воспользовавшись встроенной функцией hist. В отличие отrandtool, она позволяетзаранее выбрать количество интервалов разбиения  . Кроме того, она дает возможность построить аппроксимирующую кривую для полученной гистограммы. Для этого надо предварительно задать  , а затем воспользоваться ещё одной функцией GUI Statistics Toolbox – polytool. Она аппроксимирует данные полиномом заданной степени, в этом случае данные берутся непосредственно из гистограммы. В результате получается сглаженная кривая распределения плотности вероятности. На Рис.5.4 приведен результат применения функций hist и  polytoolк гистограмме Рис.5.2.

 

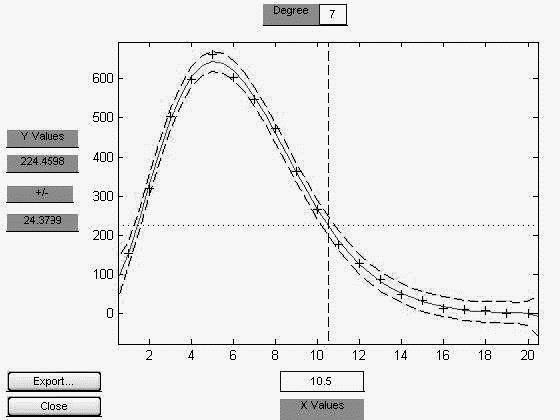              Рис.5.4. Аппроксимация распределения Релея по гистограмме Рис.5.2.

   Поясним назначение кнопок в окне этой функции. Верхняя кнопка – выбор степени аппроксимирующего полинома, в данном случае аппроксимация выполнена полиномом седьмой степени. Кнопка по центру внизу – указатель положения передвижного визира (в данном случае оно равно 10.5). С его помощью можно прочитать точные значения графика по вертикальной шкале (в нашем случае 224.4598). Назначение других кнопок читателю предлагается изучить самостоятельно в ходе ознакомления с этой функцией в МАТЛАБ.

Задание 5.3. Подробнее изучите функции hist и  polytoolпо справочному руководству МАТЛАБ, постройте такие же графики аппроксимации гистограмм для некоторых других распределений по согласованию с преподавателем.

   Генерация случайных чисел по заданному типу распределения. Существует ещё один  способ получения файлов случайных процессов с заданным законом распределения. Список возможных типов распределений  и их названий приведен в Приложении 1.

  Получить массив данных с любым типом распределения из этого списка можно функцией, образованной слиянием первых букв названия закона и окончания rnd. Например, функция exprnd(1,5000,1) выдаст вектор случайных чисел с экспоненциальным распределением плотности вероятности с одним столбцом и значением математического ожидания равным 1 (подробности см. в справочной документации МАТЛАБ). Гистограмма полученного распределения показана на Рис.5.5:

 

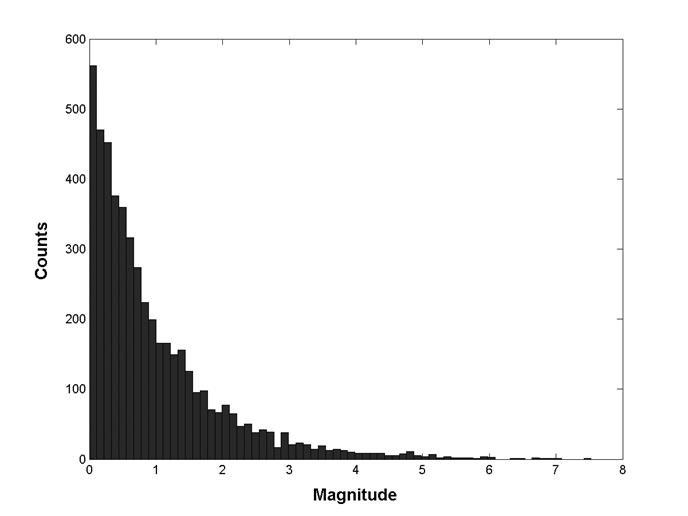Рис.5.5. Гистограмма функции распределения файла exprnd

   Дескриптивная статистика.    Обратимся теперь к описанию упомянутой выше дескриптивной (описательной) статистики, представленной в Statistics Toolbox.  Её функции возвращают конкретные значения параметров, характеризующих случайный процесс. Их список приведен в Приложении 2.   Наиболее важными параметрами в этой таблице являются :

1. Арифметическое среднее (математическое ожидание)
2. Коэффициент корреляции
3. Оценка матрицы ковариаций
4. Оценка коэффициента эксцесса
5. Медиана
6. Оценка центрального момента произвольного порядка
7. Размах выборки
8. Выборочная процентная точка (процентиль)
9. Оценка коэффициента асимметрии
10. Оценка среднеквадратичного отклонения
11. Оценка дисперсии

   Часть  указанных параметров рассмотрена нами в теоретической части описания. О других параметрах можно прочитать в справочной документации МАТЛАБ.

   Для примера вычислим математическое ожидание выборки, по которой построена гистограмма Рис.5.5. Расчет по функции mean дает значение 1.0518, что с большой точностью соответствует модельному параметру среднего , который был задан единицей.