Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 10

   Для того чтобы определить статистические параметры огибающей и начальной фазы узкополосного процесса (4.7) , поставим в соответствие вещественному случайному процессу x(t) некоторый комплексный случайный процесс, определённый  следующим образом:

                                                                                    (4.8)   

   где  сопряженный процесс, реализации которого связаны с реализациями   

преобразованием Гильберта:

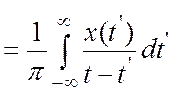                                                                             (4.9)

   В теории узкополосных случайных процессов доказывается, что с помощью сопряженного сигнала можно определить  мгновенные значения огибающей и полной фазы узкополосного сигнала (4.7):

                                                 

                                      

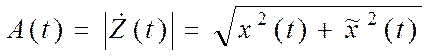
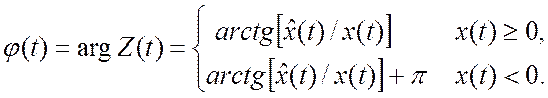
    Можно показать, что вычисленные сопряженные процессы в совпадающие моменты времени некоррелированы. Кроме того, они имеют нормальное распределение плотности вероятности. Можно огибающую A(t) пронормировать на её среднеквадратичное значение, то получится безразмерная случайная функция    . Как показывает теория, плотность вероятности величины имеет вид:

                                                                      (4.10)

это известное распределение Рэлея. График этого распределения показан на Рис. 4.4.

 

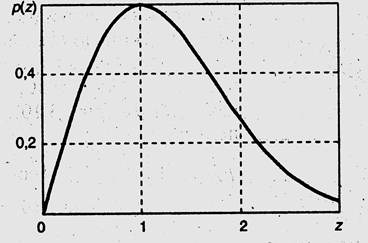                        Рис.4.4. Плотность вероятности огибающей узкополосного

                                       случайного процесса (распределение Релея)

      Из графика видно, что наиболее вероятны  значения амплитуды порядка её среднеквадратичного значения. В то же время маловероятно, чтобы огибающая принимала значения близкие к нулю, или  очень большие значения, сильно превосходящие среднеквадратичный уровень.

   Узкополосный случайный процесс при наличии детерминированной составляющей. Если узкополосный процесс содержит детерминированную составляющую (например, к нему примешана гармоническая компонента),  то плотность вероятности  огибающей подчиняется    распределению Релея – Райса      [ 3 ]:

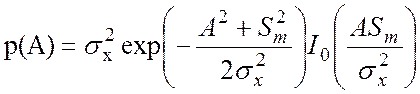                                                                  (4.11)  

где 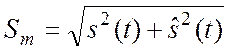 – амплитуда огибающей детерминированной компоненты сигнала в данный момент времени,  –  дисперсия,  – функция Бесселя нулевого порядка от мнимого аргумента. На Рис. 4.5 показаны графики данной плотности вероятности для различных соотношений – амплитуды детерминированной компоненты к среднеквадратичному уровню  случайной компоненты.    

 

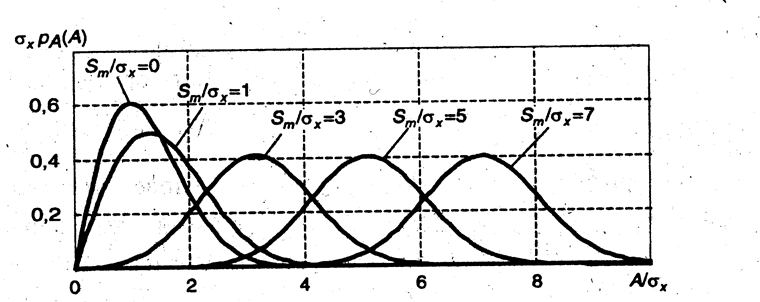Рис.4.5. Плотность вероятности огибающей узкополосного  шума при      

наличии детерминированной составляющей (гармонического сигнала)

   Из Рис.4.5  хорошо видно, что при отсутствии гармонической компоненты  распределение переходит в распределение Релея, а при большой амплитуде этой компоненты распределение стремится к нормальному.

   Проведенное рассмотрение охватывает лишь самые начала теории случайных процессов.Более подробное изложение этой теории можно найти в   [ 3 ], [ 5 ], [ 6 ] и др. Обратимся теперь  к примерам статистического описания конкретных случайных процессов. Для этого рассмотрим возможности моделирования процессов с различными функциями распределения  вероятности, генерации соответствующих им цифровых реализаций сигналов, вычисления некоторых модельных параметров процессов.

Раздел 5. МЕТОДЫ МОДЕЛИРОВАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ 

В системе МАТЛАБ существует пакет расширения Statistics Toolbox. Он представляет    собой набор программ, ориентированных на весьма широкий спектр задач – от генерации сигналов с заданными функциями распределения и подбора кривых под экспериментальные данные, до планирования экспериментов и задач промышленного статистического контроля. Набор функций этого расширения весьма обширен, в последних версиях МАТЛАБ  их свыше двухсот. Мы ограничимся изучением некоторых из них, это позволит глубже понять теоретический материал, изложенный выше. По ходу изложения будем формулировать конкретные задачи , которые необходимо будет выполнить в ходе реботы.