Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 11

Пакет расширения  Statistics Toolbox снабженудобным интерфейсом пользователя (GUI), он предназначен для выведения графиков функций распределения плотности вероятности, генерации соответствующих им файлов данных и подбора аппроксимирующих кривых для экспериментальных данных, распределение которых заранее не известно. В расширении Statistics Toolbox содержится также набор функций описательной или дескрипторной статистики случайных процессов. Имеются также функции, осуществляющие кластерный анализ, регрессионный анализ, проверку гипотез о свойствах распределений, метод главных компонент и др. (эти методы в данной лабораторной работе не отражены ввиду ограниченности объема). Ознакомиться  с ними  можно, например, в [ 9 ].

   Прежде всего, расширение  Statistics Toolbox  предоставляет возможность просмотра графиков функций распределения плотности вероятности большинства процессов, встречающихся на практике. Просмотр графиков распределений  вызывается функцией disttool,  она позволяетизучать интегральные и дифференциальные функции  распределения вероятностей для 19 теоретических законов распределения.

   Для примера на Рис.5.1 приведен график распределения плотности вероятности Релея, полученный с помощью этой функции. Рис.5.1 соответствует дисперсии процесса равной двум. Графический интерфейс  функции содержит кнопку, с помощью которой можно получать графики распределений для различных дисперсий. На изображении имеется подвижный визир, отмеченный пунктиром. Передвигая его вдоль оси  можно исследовать детали распределения.

Замечание.К сожалению, в списке распределений,

представленных в программе disttool,  отсутствует важное  распределение Релея –Райса.

 

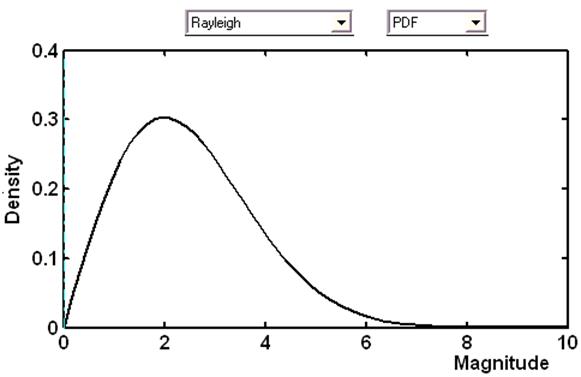                  Рис.5.1. Плотность вероятности Релеевского распределения

    Задание 5.1.Пользуясь приложением disttoolтщательно изучите нормальное (Гауссово) распределение, Релеевское распределение и распределение Пуассона как наиболее часто встречающиеся в практических приложениях. Необходимо построить их графики при разных значениях параметров.

   Далее, в GUI Statistics Toolbox входит программа генерации случайных чисел с заданным законом распределения. Она генерирует цифровую  реализацию соответствующего случайного процесса. Её вызов осуществляется командой randtool , которая возвращает гистограмму соответствующего распределения плотности вероятности. Пример её использования показан на Рис.5.2, где отражена гистограмма распределения плотности вероятности сгенерированного файла данных с релеевским распределением. Длина реализации – 5000 чисел. Гистограмма построена с разбиением амплитуд сигналов на тридцать уровней. Полезно сравнить Рис.5.2 с теоретической кривой Рис.5.1, видно их несомненное сходство.

   Для дальнейшей обработки можно вывести модельный файл реализации этого процесса  с помощью кнопкиExport(илиOutputв более ранних версиях МАТЛАБ). Она экспортирует реализацию непосредственно в рабочую область МАТЛАБ в виде специальной переменной, в данном случае raylrv,  её можно переобозначить и сохранить в отдельном файле.

   Для каждого вида распределений имя этой переменной своё, её первые буквы включают сокращенное имя распределения (в последних версиях МАТЛАБ ей сразу можно присваивать любое название). Поскольку она находится в рабочей области МАТЛАБ, дальше её можно обрабатывать независимо от Statistics Toolbox. Для примера на Рис.5.3 показан график фрагмента  изучаемого релеевского  процесса.

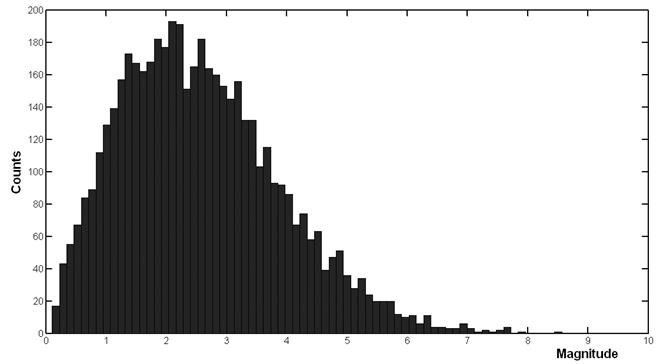
Рис.5.2. Гистограмма распределения плотности вероятности для модельного файла с релеевским распределением плотности вероятности.

Любопытно отметить, что функция randtoolсама выбирает количество интервалов разбиения гистограммы по уровням . Оно зависит от количества отсчетов в файле (объема выборки) samples. По умолчанию samples= 100 и 10. В нашем случаеsamples= 5000,соответственно 70. Это означает, что чем больше объем выборки, тем точнее формируется оценка её плотности вероятности.