Примечание: Разновидность анализа случайных процессов, при котором изучаются только математическое ожидание, дисперсия и автокорреляционная функция, называют, для краткости, корреляционным анализом. В ряде случаев такого анализа вполне достаточно.
Нормальный случайный процесс. Нормальный (гауссовский) закон распределения плотности вероятности случайных величин (или процессов) является самым распространенным в практике физических измерений. Одномерная плотность вероятности стационарного нормального процесса определяется выражением:
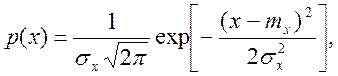(3.4)
где 
и 
– соответственно, математическое ожидание
и дисперсия процесса.
Широкое распространение нормального закона распределения в природе объясняется тем, что при суммировании достаточно большого числа равновеликих статистически независимых случайных величин (и процессов), имеющих произвольные плотности распределения вероятности, плотность распределения суммы стремится к нормальной. Это положение носит название центральной предельной теоремы [ 3 ].
На Рис.3.1 изображена плотность вероятности случайной величины с нормальным законом распределения:
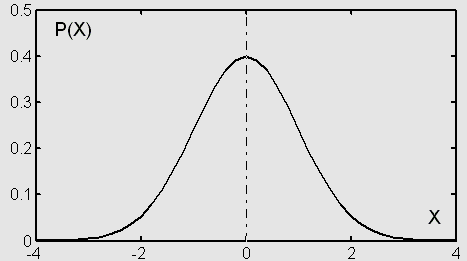
Рис.3.1. Нормальный (гауссовский) закон распределения плотности вероятности
Весьма полезным свойством нормального распределения (и только его) является то, что из некоррелированности гауссовых случайных величин (и процессов) следует их статистическая независимость. Кроме того, они полностью описываются в рамках корреляционного анализа.
Важной особенностью нормальных процессов является равенство нулю коэффициентов асимметрии и эксцесса (1.14). Определяя экспериментальные значения этих коэффициентов можно судить о степени отличия плотности вероятности исследуемого процесса от нормального закона.
Раздел 4. СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
Следует обратить внимание на то, что данные о распределении вероятности случайных процессов не дают никаких сведений о поведении случайного процесса во времени. Корреляционная функция характеризует лишь степень статистической связи значений в разные моменты времени. Для детерминированных сигналов их временная структура хорошо описывается в рамках спектральной теории. Существует ли аппарат анализа спектральных свойств случайных процессов? Да, он существует, но совершенно не в той форме, что для детерминированных сигналов.
Заметим, что каждая отдельно взятая реализация случайного процесса представляет собой детерминированную функцию, и к ней можно применить преобразование Фурье. При этом различные реализации будут, естественно, иметь различные спектры. Нас же интересуют статистически усредненные характеристики случайных процессов. Попытаемся найти среднее значение спектральной плотности случайного процесса (горизонтальной чертой здесь и далее обозначается операция статистического усреднения по ансамблю реализаций):
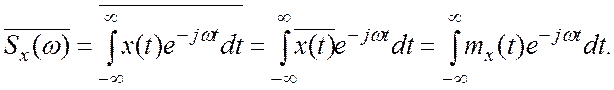
Как видно из этой формулы, усредненная спектральная плотность случайного процесса представляет собой спектр его математического ожидания. Для центрированных процессов mx(t) = 0. Таким образом, усредненное значение спектральной плотности не несет никакой информации о флуктуационной, т. е. собственно случайной, составляющей случайного процесса. Это происходит потому, что фазы спектральных составляющих в различных реализациях процесса случайны и независимы.
Можно, однако, рассмотреть спектральную плотность мощности случайного процесса, поскольку мощность не зависит от соотношения фаз спектральных составляющих.
Рассмотрим центрированный случайный процесс и выделим из его ансамбля какую-либо реализацию x(t) , ограничив ее длительность конечным интервалом времени
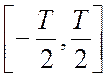
Применив затем к этой реализации прямое преобразование Фурье, найдем ее
спектральную плотность
. Энергию ЕТ рассматриваемого отрезка
реализации согласно
равенству Парсеваля можно вычислить как
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.