Автоматизированные измерения и моделирование свойств случайных процессов: Учебно методическое пособие, страница 14

1.  Цифровой осциллоскоп с одновременным выводом на экран дисплея четырех осциллограмм сигналов.

2.  Спектроанализатор с заданными параметрами спектрального анализа.

3.  Устройство регистрации цифровых реализаций сигналов одновременно по

            ряду каналов, от одного до шестнадцати.

4.  Просмотр зарегистрированных реализаций.

   Внешний вид экрана дисплея в режиме  "Осциллоскоп" показан на Рис.6.2. Активным является один канал, на нем развернута осциллограмма случайного сигнала, взятого с  лабораторного генератора шума .  По Рис.6.2 можно визуально оценить некоторые характеристики процесса, например, его максимальную амплитуду.

 

  Рис.6.2. Осциллограмма случайного сигнала в режиме "Осциллоскоп";  по горизонтали

– шкала времени (в мс), по вертикали – шкала амплитуд (один вольт на деление).

   Представляет интерес определить "размах" между максимальными и минимальными значениями сигнала. Такие "прикидочные" измерения весьма полезны на практике. В статистике это называется "разведочный анализ". Например, если процесс нормальный, то его дисперсия примерно равна одной трети  размаха амплитуды. Это вытекает из свойств нормального распределения [ 3 ].

   Рассмотрим работу L-761 в режиме "Спектроанализатор". На Рис.6.3 показана единичная спектрограмма случайного процесса, показанного ранее на Рис.6.2.  По горизонтали отложены значения частоты (в условной шкале). Интенсивность спектра откладывается  по вертикальной шкале в логарифмическом масштабе.   В верхнем узком окне Рис.6.3 открывается осциллограмма исходного анализируемого процесса.

   Видно, что спектр сильно флуктуирует, поскольку его оценка сама является случайной величиной, но уже в частотной области. Подробнее этот вопрос обсуждается в описании упомянутой лабораторной работы "Методы определения спектральных характеристик электрических сигналов". Здесь мы лишь отметим, что получение надежных оценок спектров случайных процессов возможно после их многократного усреднения по ряду спектрограмм. Устройство L-761 позволяет провести такое усреднение, результат его показан на Рис.6.4.

   В нижней части Рис.6.4 выводится вспомогательная информация, из которой видно, что усреднение произошло по 1863-м единичным спектрограммам. Заодно отметим, что преобразование Фурье выполнялось по 256 точкам, использовалось окно Блэкмана –Харриса ( подробности см. в упомянутой лабораторной работе)., тип выводимого спектра – модуль спектральной интенсивности (амплитуды на каждой элементарной частоте). Чтобы перейти к обычному спектру мощности надо их возвести в квадрат. Поскольку вертикальная шкала Рис.6.4 отложена в логарифмическом масштабе, достаточно её значения просто удвоить.

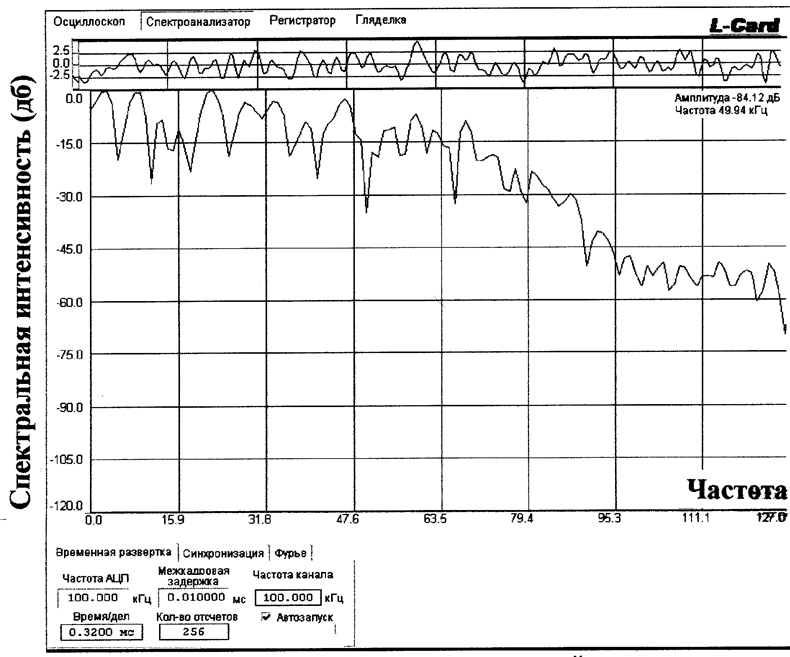
Рис.6.3. Неусредненная  спектрограмма случайного процесса.

 

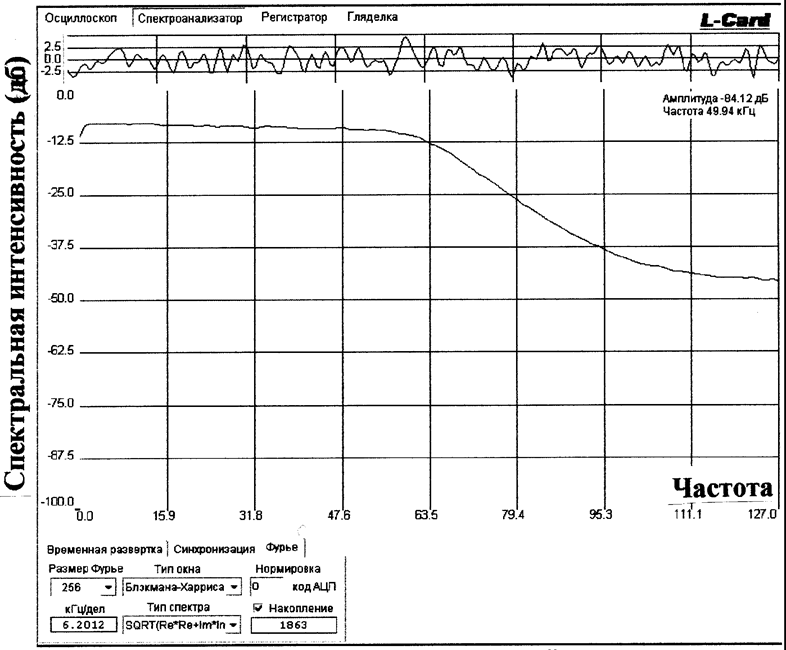Рис.6.4. Усредненная спектрограмма того же процесса.

Примечание.К сожалению, градуировка вертикальной шкалы спектрографа в линейном масштабе не предусмотрена. Логарифмический масштаб удобен  для одновременного анализа и больших, и малых компонент спектра, но каждый раз требует перевода в обычную шкалу, если их сравнивать в линейном масштабе.

   Как видно из Рис.6.4 флуктуации результирующей спектрограммы практически исчезли и выявилась важная закономерность: интенсивность шума неравномерна по частоте.  Это возникло из-за наличия в тракте лабораторного генератора шума встроенного  фильтра нижних частот (он формирует полосу шума "0–20кгц"). По рис.6.4 работу этого фильтра можно оценить детально. Сделаем это.