Сущность и особенности проблемы электромагнитного взаимодействия радиоэлектронного оборудования, страница 24

По аналогии с предыдущими выкладками получим:

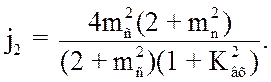                                                           (3.92)

При , (3.92) преобразует к виду:

                                                                       (3.93)

Из (3.85) следует, что при отсутствии модуляции на выходе ЛД подавляется составляющая

с .

При анализе функционирования цифровых систем критерий УКП записывается в виде:

                                                                               (3.94)

где ,- вероятности ошибок передачи информационного сообщения в случае отсутствия и наличия помеховых воздействий соответственно.

Будем считать, что полезный сигнал модулирован по амплитуде двоичным цифровым сообщением и имеет место одновременное воздействие помех и внутренних шумов. Необходимо отметить, что в данном случае на выходе ПРМ находиться решающее устройства (РУ), работающее по методу стробирования, т.е. анализирующее напряжение ЛД (демодулятора) в моменты времени, соответствующие . где Т – промежуток времени между отсчётами, а - время, соответствующее положению символа в тактовом интервале. Полезный сигнал на входе детектора в соответствии с [17] запишем в виде:

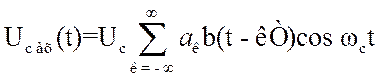                                          (3.95)

где     - функция, определяющая форму огибающей символа на входе;

- дискретная величина, принимающая значение, равное либо , либо ;

К- номер символа.

В свою очередь, НЭМП на входе детектора:

                                         (3.96)

где     - начальная фаза;

-случайный процесс, характеризующий фазовую модуляцию помехи.

С учетом   и вводя обозначение

                                                               (3.97)

Запишем (3.96) в виде:

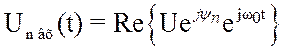                                                         (3.98)

Введем определение, характеризующее сумму сигнал + помеха, аналогичное (3.13):

                                          (3.99)

При условии, что , собственные шумы на входе ЛД можно считать узкополосным стационарным случайным процессом, имеющим нормальное распределение [3]

                                                                                (3.100)

Здесь  и  - нормальные случайные стационарные процессы с одинаковой дисперсией , равной дисперсии процесса .

Определим вероятность ошибки при приеме символа с номером соответствующим паузе . При этом.

Очевидно, что данная ошибка (ложные тревоги) может иметь место в том случае, когда на входе ЛД напряжение , определяемое в общем случае С, П и Ш, превысит некоторое пороговое напряжение  РУ, т.е. при условии:

.

Учитывая независимость процессов, определяющих , и усреднений по всем возможным значениям, запишем:

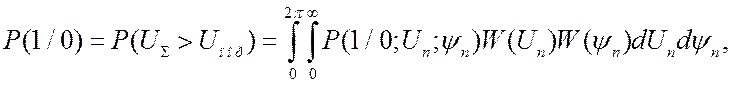                                                                                               (3.101)

где      - функция распределения огибающей помехового сигнала на входе ЛД;

           - вероятность условий ошибочного приема при фиксированных значениях  и  соответственно.

Функция плотности вероятности огибающей суммарного сигнала распределена по обобщенному закону Рэлея:

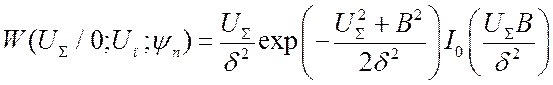.                                                                                               (3.102)

При известных значениях полосы пропускания  и энергетического спектра  дисперсия собственных (тепловых) шумов равна: .

Учитывая (3.102), имеем:

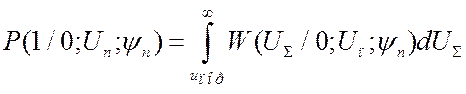.                                                                                               (3.103)

Интеграл в правой части (3.103) с учетом (3.102) может быть представлен через функцию распределений Райса-Релея – это справочная -функция [9].

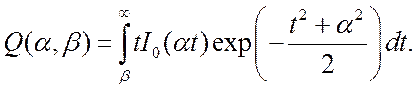                                                                                               (3.104)

Тогда:

                                                                                               (3.105)

Следует отметить, что процесс  будет иметь равномерное распределение на интервале . Это следует из (3.96), т.к.  также имеет равномерное распределение в интервале . Таким образом:

.                                                                                               (3.106)