Из [3] имеем
![]() , (3.23)
, (3.23)
где Ф[…] – нормированная функция Лапласа;
![]()
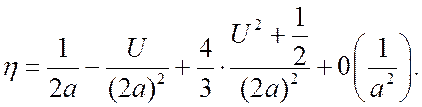
При определении
вероятности совпадения импульсов сигнала или помехи ![]() была
такой, при которой исключалось бы срабатывание порогового устройства на выходе
приемника.
была
такой, при которой исключалось бы срабатывание порогового устройства на выходе
приемника.
На рис. 3.8 представлены возможные случаи расположения рассматриваемых сигналов.
Очевидно, что
границы изменения длительности импульсов помехи при фиксированной длительности
сигнала, составляют ![]() и
и ![]() , а
передний фронт импульса помехи будет находиться в пределах
, а
передний фронт импульса помехи будет находиться в пределах ![]() . При иных условиях
. При иных условиях ![]() будет
срабатывание порогового устройства и неперекрытая часть импульса помехи или
сигнала будет восприниматься как импульс сигнала за счет интервалов
стробирования дешифратора
будет
срабатывание порогового устройства и неперекрытая часть импульса помехи или
сигнала будет восприниматься как импульс сигнала за счет интервалов
стробирования дешифратора ![]() . Считая поток
импульсных помех пуассоновским, имеем
. Считая поток
импульсных помех пуассоновским, имеем
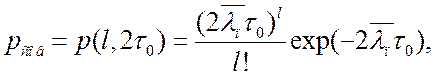 (3.24)
(3.24)
где ![]() -
вероятность того, что на интервале
-
вероятность того, что на интервале ![]() появляется
появляется ![]() импульсов;
импульсов;
![]() -
средняя частота импульсов помехи.
-
средняя частота импульсов помехи.
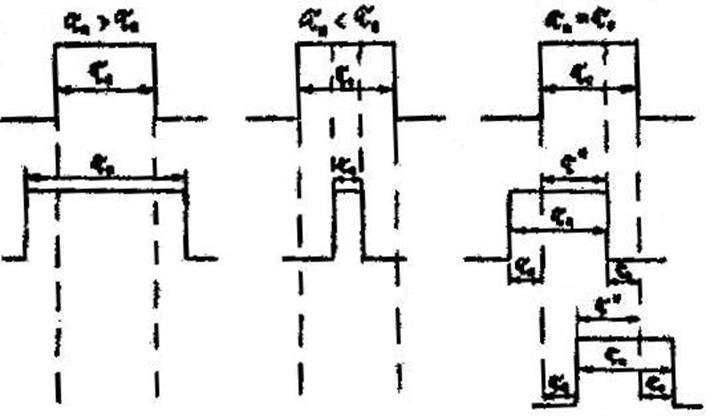
Рис. 3.8. Совпадение импульсов сигнала и помехи
(![]() ,
, ![]() -
длительности импульсов сигнала и помехи соответственно.
-
длительности импульсов сигнала и помехи соответственно. ![]() - длительность перекрытия импульсов)
- длительность перекрытия импульсов)
Считая, что
вероятность появления более одного импулься НЭМП на интервале ![]() мала, получаем
мала, получаем
![]() (3.25)
(3.25)
Раскладывая в
(3.25) ![]() в степенной ряд, получаем расчетное
соотношение
в степенной ряд, получаем расчетное
соотношение
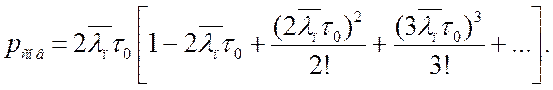 (3.26)
(3.26)
Вероятность интерференционного сбоя полезного сигнала импульсной помехой определяется в виде
![]() , (3.27)
, (3.27)
где ![]() вероятности
близких амплитудных значений;
вероятности
близких амплитудных значений;
![]() вероятности противофазности высокочастотного
заполнения;
вероятности противофазности высокочастотного
заполнения;
![]() вероятности того, что при
вероятности того, что при ![]() и
и ![]() , условия подавления импульса практически неизменны.
, условия подавления импульса практически неизменны.
При условии
близких значений амплитуд рассматриваемых сигналов и выполнения условия ![]() , можно записать
, можно записать
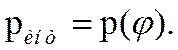 (3.28)
(3.28)
Для определения ![]() рассмотрим два монохроматических колебания
рассмотрим два монохроматических колебания ![]()
![]() и
и ![]() . Пусть
относительная величина порога равна
. Пусть
относительная величина порога равна ![]() . Очевидно, что идеальная
значения фазового сдвига между рассматриваемыми колебаниями равны
. Очевидно, что идеальная
значения фазового сдвига между рассматриваемыми колебаниями равны
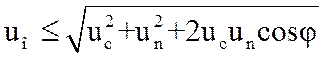 . (3.29)
. (3.29)
Введем
обозначение ![]() и преобразуем (3.29) к виду
и преобразуем (3.29) к виду
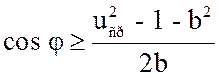 , (3.30)
, (3.30)
откуда получим
![]()
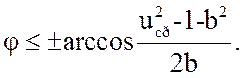 (3.31)
(3.31)
Очевидно, что при выполнении условий (3.30) и (3.31) подавления сигнала не происходит. Последние возможно при
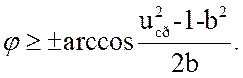 (3.32)
(3.32)
Считая, что
величина фазового сдвига между некоррелированным сигналом и помехой
распределена равномерно в ![]() , получаем
, получаем
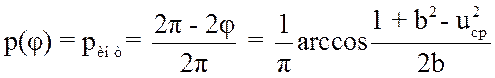 (3.33)
(3.33)
Так как ![]() , то
, то
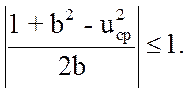 (3.34)
(3.34)
Определим
соотношение между ![]() и
и ![]() при
интерференционном подавлении. Из (3.34) имеем
при
интерференционном подавлении. Из (3.34) имеем
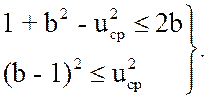 (3.35)
(3.35)
Решая (3.35), получим
![]() (3.36)
(3.36)
![]() (3.37)
(3.37)
![]() (3.38)
(3.38)
![]() . (3.39)
. (3.39)
Из (3.36). (3.37) и (3.39) (исключая
(3.38) неопределенность) имеем![]() ;
; ![]() и
и ![]()
Объединяя, получаем
![]() (3.40)
(3.40)
или
![]() . (3.41)
. (3.41)
Таким образом, интервал изменений
амплитуды помехи, который может вызвать подавление, получается равным
удвоенному значению порогового напряжения ![]() .
.
С учетом приведенных соотношений, получим

![]()
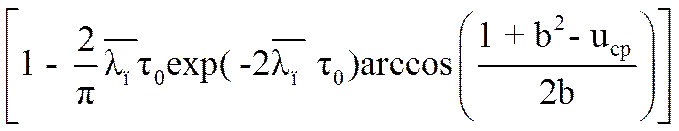 . (3.42)
. (3.42)
Для бинарного сигнала имеем
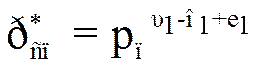 , (3.43)
, (3.43)
где
![]() - число нулевых позиций в синхрогруппе бинарного
сигнала;
- число нулевых позиций в синхрогруппе бинарного
сигнала;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.