Сущность и особенности проблемы электромагнитного взаимодействия радиоэлектронного оборудования, страница 21

- число единичных позиций в информационной группе.

Величина - переменная и её значения  могут меняться от нуля до . Поэтому полная вероятность прохождения сигнала через приёмник равна

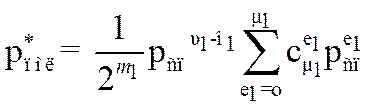                                          . (3.44)

Воспользовавшись биномом Ньютона, получим

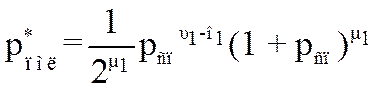                                          ,  (3.45)

где описывает соотношением (3.42).

Для рассматриваемой ситуации представляет интерес выяснение среднего числа срабатывания решающего устройства (N) за интервал наблюдения T. При условии независимости воздействующих  сигналов получим

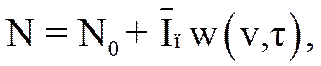                                                   (3.46)

где   - среднее значение срабатываний решающего устройства от шумов за время Т;

- среднее количество импульсов помехи на входе приёмника за время Т;

 - вероятность прохождения импульсной помехи;

- длительность импульсной помехи.

Из [48] для средней частоты выбросов огибающей нормального шума и гармонического сигнала над уровнем  с учетом допущения имеем:

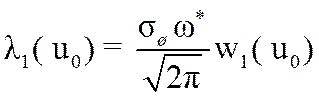                                              ,     (3.47)

где     ;

          - ширина полосы пропускания приемника;

- плотность вероятности огибающей нормально шума и гармонического сигнала.

Считая, что выбросы над уровнем распределены по законы Пуассона [21], будем иметь

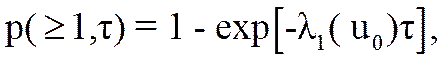
где  - длительность временного интервала, равная длительности импульса помехи. С учетом сделанных допущений запишем (3.36) в виде

                                                                           (3.48)

Определяя составляющие (3.48) предварительно отметим тот факт, что внутренние и внешние шумы приёмника являются независимыми и, следовательно, для дисперсии огибающей аддитивного шума верно соотношение

Из [3] имеем

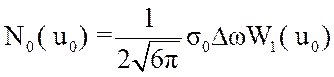                                                 (3.49)

где - плотность вероятности для значения шума, равного .

При прохождении через узкополосные фильтры приёмника шум нормализуется, решающее устройства стоит после детектора, то в соответствии с распределением Релея

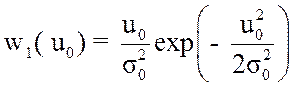                                               .       (3.50)

Подставляя (3.50) в (3.49) и введя обозначение  получаем

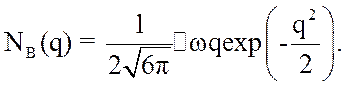                                                (3.51)

Существующие пороговые устройства срабатывают только от выбросов, длительности которых не менее вполне определенной величины . Тогда (3.51) запишем в виде

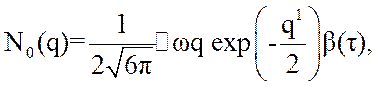                                          (3.52)

где - вероятность того, что длительность выброса не менее . Плотность распределения длительностей выбросов случайного процесса, которая для огибающей нормального узкополосного стационарного шума определяется в соответствии с [17] как

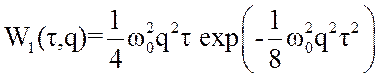                                          (3.53)

позволяет рассчитать  в (3.53)

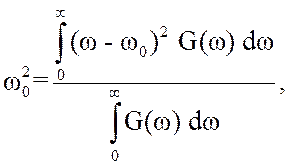                                                        (3.54)

где     - энергетический спектр шума;

          -рабочая частота УПЧ.

Считая постоянной в пределах полосы пропускания приемника, имеем

,        ;

,                   .

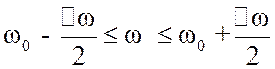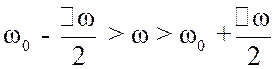Из (3.54) находим 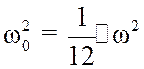 и подставляя в (3.53), получаем выражение для плотности распределения длительности выбросов шума над относительным порогом

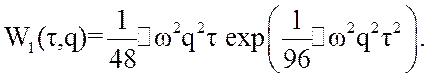                                                                                                      (3.55)

С учетом (3.55) имеем

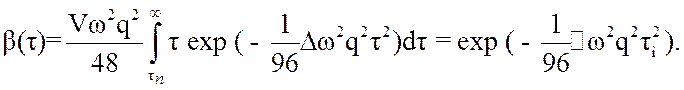                                                                         (3.56)

Подставляя (3.56) в (3.52), окончательно получаем

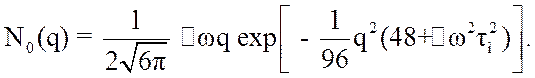                                                                                              (3.57)

Результаты экспериментальных исследований подтверждают высокую достоверность найденного выражения. Для определения воспользуемся соотношением (3.23). Полагая  и  где -амплитуда импульсной помехи, будем иметь

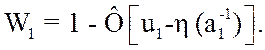                                                           (3.58)

Обозначим среднее количество импульсов помехи, вызвавших срабатывание решающего устройства, через . Тогда

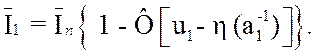                                                    (3.59)

Подставляя (3.57) и (3.58) в (3.48), получаем для среднего количества срабатываний решающего устройства от шумов и помех