Сущность и особенности проблемы электромагнитного взаимодействия радиоэлектронного оборудования, страница 17

Обозначим через P(a) и P(c) вероятности того, что в момент времени t,  0<t<T значения выходного сигнала U_вых(t) попадают во внешние области A и С; P(b) соответственно в B, а через ,  и  аналогичные состояния для сигнала . Расхождения соответствующих вероятностей можно оценить следующим образом

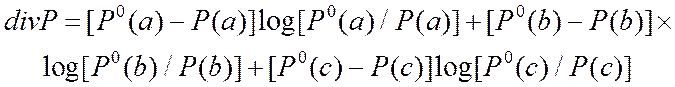                                                                                      (3.1)

Выражение (3.1)  косвенным образом учитывает нелинейные свойства приемо-анализирующих трактов РЭС (X и Y имеют смысл порога), оно обращается в ноль при равенстве соответствующих вероятностей. Следовательно, ЭМО тем благоприятнее, чем меньшее значение выражения (3.1).

Данные для определения  можно получить, заменяя исследуемые процессы ,  последовательностью случайных событий, характеризующимися тремя возможными, но несовместимыми событиями A, B и С (рис. 3.3 б, в, г).  При этом определяют вероятности перехода или неперехода из одного состояния в другое и находят переходные вероятности, применяя аппарат конечных цепей Маркова [21] к принятой модели исследуемых процессов  и .

Обозначим через  и  среднее число пересечений анализируемым процессом U_вых(t) уровней X и Y снизу и сверху соответственно. При этом число  равно количеству событий , характеризующихся состоянием,   : , а  и   :  на интервале наблюдения. Разобъем отрезок T на  таких коротких интервалов времени , что внутри любого из них анализируемый процесс не может изменить своего состояния более одного раза. Импульсы с длительностью  называются опорными или счетными (рис. 3.3 б, в, г, д). При этом события  , , ,  и  рассматриваются как чередующиеся группы счетных импульсов. Случайные серии опорных импульсов можно рассматривать как простые марковские цепи, которым соответствует граф на рис. 3.5.

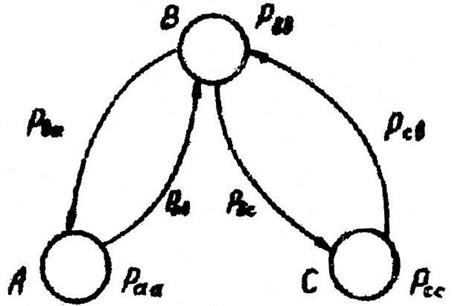
Рис. 3.5. Сигнальный граф переходных вероятностей пересечения уровней

Переходные вероятности, соответствующие этому графу, запишем в виде -матрицы:

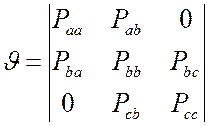,                                                       (3.2)

а начальное состояние в виде:

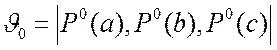.                                                 (3.3)

Пусть , принимаемый за начало отсчета, процесс характеризовался событием . Тогда вероятность того, что -м окажется импульс, соответствующий событию , определится как соответствующий элемент матрицы следующего вида:

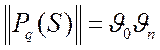.                                                                                                   (3.4)

Переходные вероятности, образующие матрицы (3.2…3.4), связаны со средними значениями  и  и количеством опорных импульсов , соответствующим наступлению событий , следующими соотношениями:

; ;;

;;.

Очевидно, что чем ниже устанавливается пороговые значения  и , тем более жесткие требования предъявляются к ЭМО.

Отметим, что . Если длительность счетных импульсов значительно меньше периода колебаний огибающей сигнала, то (3.4) упрощается и преобразуется в условные вероятности:

                                                                                                           (3.5)

3.2. Особенности учета уровня межсистемных помех

При оценке допустимого уровня помех, воздействующих на конкретную радиотехническую систему, находят из допусковых норм изменения выходных характеристик системы, численное значение которых определяется выходным отношением сигнал/помеха.

Раздели помехи сосредоточенные по спектру и во времени. Очевидно, что первые представляют собой ансамбль узкополосных сигналов, излучаемых РЭС. Представим -й узкополосный сигнал в виде:

,                                                                                                   (3.6)

где 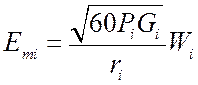     - амплитудное значение напряженности поля -го сигнала в точке приема;

           - мощность, подводимая к антенне -го источника НЭМП;

           - расстояние от -го источника до точки приема, м;

           - коэффициент усиления -й антенны, =В/м;

           - множитель ослабления, учитывающий высоты поднятия антенн, вид поляризации, параметры почвы и т.д.