Сущность и особенности проблемы электромагнитного взаимодействия радиоэлектронного оборудования, страница 11

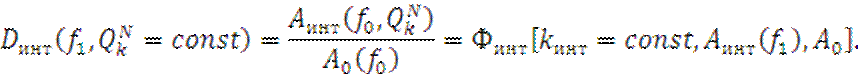
Заметим, что в дальнейшем все оценки ХЧИ и расчёт параметров ЭМС будет прводиться для типовой схемы радиоприёмного устройства, изображённого на рис. 1.7

Рис. 1.7. Типовая схема приёмника

2.  МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ АМПЛИТУДНОЙ И ЧАСТОТНОЙ ОЦЕНКИ ВОСПРИИМЧИВОСТИ ПРИЁМО-АНАЛИЗИРУЮЩИХ ТРАКТОВ ПО ПОБОЧНЫМ КАНАЛАМ ПРИЁМА.

2.1.  Модели оценки характеристик частотной избирательности

Оценки ХЧИ по СКП. Предположим, что динамический диапазон по ОКП известен, а не ПРМ воздействуют внутренние шумы со спектральной плотностью N₀ и мешающий сигнал на частоте СКП:

(2.1)

где    - частотный разнос между каналами;  - частотный резонанс, соответствующий коэффициенту прямоугольности    на фиксированном уровне .

Для схемы, изображённой на рис.1.7. отношение С/(Ш+П) на выходе СФ (ведь это УПЧ) будет равно:

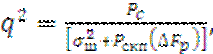                                                          (2.2)

где   - мощность внутренних шумов на выходе ПРМ;  - нормированная АЧХ ПРМ (УПЧ).

Мощность сигнала на выходе ПРМ в соответствии с [8] равна:

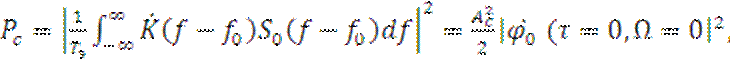                                                                                           (2.3)

где   - нормированная ковариационная функция сигнала;  - разность соответствующих параметров принимаемого и опорного сигналов; мощность помехового сигнала (2.1) по СКП на выходе ПРМ –

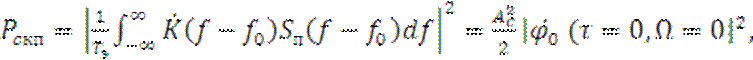                                                                                                           (2.4)

где  - эффективная длительность сигнала;  и - спектры полезного и мешающего сигналов;  - нормированная корреляционная функция, её квадрат является функцией неопределённости.

При совпадении модулирующих функций  и   

Подставляя (2.3) и (2.4) в (2.2), получаем:

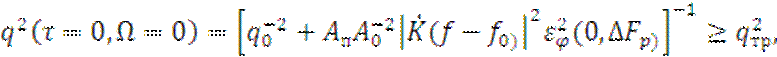                                                                                                 (2.5)

где   – отношение (С/Ш) вх;  - требуемое отношение С/(П+Ш), определяемое заданным уровнем качества функционирования ПРМ;        .

С учётом (1.7) и (2.5) имеем

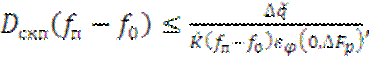(2.6)

где 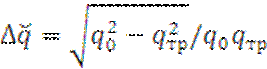  – допустимое относительное изменение отношения С/(П+Ш) на выходе при наличии помех по СКП.

Очевидно, что для широкополосного сигнала динамический диапазон ПРМ с СФ будет в  раз больше и может достигать значений коэффициента сжатия (базы) сигнала .

Из (2.6) следует зависимость  от формы АЧХ УПЧ - , т.е. от коэффициента прямоугольности как параметра ХЧИ. Для точки частотного диапазона  получаем

(2.7)

При этом определённому значению параметра  соответствует определённое значение , которое зависит от числа контуров в УПЧ и их частотной расстройки друг относительно друга, что показано на рис. 2.1.

Из рис. 2.1 следует, что при h= 5 … 6 , т.е. при чувствительности ПРМ, равной А₀ = В, восприимчивость к НЭМП по СКП А_п < 0,1 … 1 В.

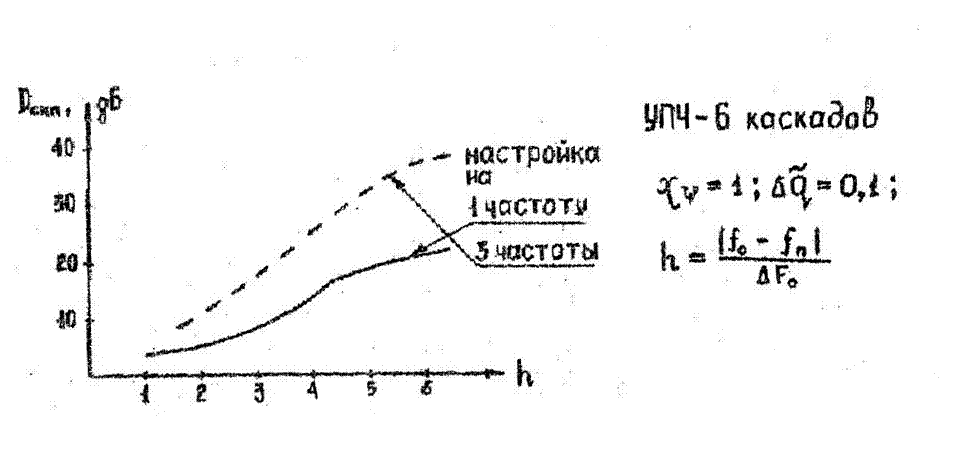
Рис. 2.1. Зависимость  от относительной расстройки h

Оценка ХЧИ по ПКП. Непосредственно в ПРМ (рис. 2.7) основным источником помех является преселектор, представляющий по отношению к f₀ линейное звено с параметрами, а по отношению к f_г нелинейное звено [13].

Выходное отношение С/(П+Ш) запишем в виде:

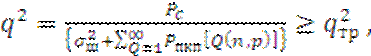                                                                  (2.8)

где   – мощность полезного сигнала и НЭМП, прошедших по ПКП; p,n - № гармоник помехи и гетеродина соответственно.

Анализ (2.8) показывает возможность оценки восприимчивости ПРМ и помехам по ПКП либо при декомпозиции последних, либо при учёте того, что НЭМП равномерно распределены по всему частотному диапазону и действуют одновременно по всем ПКП.

Оценим динамический диапазон ПРМ по ПКП (n+p) – го порядка. Обозначим крутизну передаточной характеристики линейной части ПРМ в рабочей точке через . При резонансный контур настроен на частоту .

Для оценки динамического диапазона необходимо знать амплитуду помехи, прошедшей через один из ПКП., например с номером, соответствующим     Q- му порядку преобразования, а также чувствительность ПРМ. Будем считать, что  , а  - известна.

Для этого случая полезный сигнал на выходе ПРМ в отсутствии НЭМП определяется в соответствии с [10]:

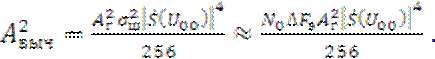                                                                      (2.10)