Сущность и особенности проблемы электромагнитного взаимодействия радиоэлектронного оборудования, страница 23

                                                       (3.69)

                                                       (3.70)

где  - i–я соответствующая модулирующая функция.

Например, при модуляции тоном частоты   при глубине модуляции m

                                                                (3.71)

Также считаем, что НЭМП частично или полностью воздействует по ОКП ПРМ, а . Опуская зависимость от t для мгновенных значений сигналов, запишем после элементарных преобразований суммарный результат входного воздействия с учетом (3.69) и (3.70) в виде:

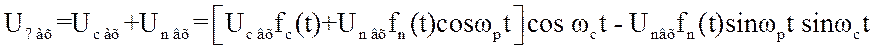
Возводя в квадрат, имеем:

                                                                            (3.72)

Введем обозначения:

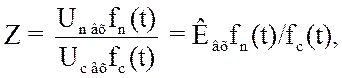                                                (3.73)

где  и

Подставляя (3.73) в (3.72) с учетом введенных переменных, получим:

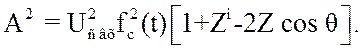                                             (3.74)

При коэффициенте передачи, равном единице, напряжение на выходе ЛД для удобства  последующих преобразований запишем следующие промежуточные переменные:

                                                 (3.75)

Тогда в соответствии с (3.74) запишем

                                                              (3.76)

В случае отсутствия модуляции сигналов, т.е. при  , а , имеем:

                                                                      (3.77)

                                                        (3.78)

При условии, что , т.е. при , величина , входящая в (3.77), может быть в соответствии с [14] представлена в виде полинома Лежандра.

С учетом (3.78) запишем:

.

Подставляя данное выражение в (3.77) и опуская запись аргумента у членов полинома, получим:

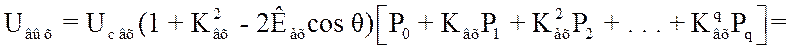
                                            (3.79)

Из [23] известно, что  тогда нетрудно заметить, что

                                                                                                     (3.80)

Кроме этого, для первых членов полинома Лежандра справедливы равенства

                                            (3.81)

После подстановки (3.80) и (3.81) в (3.79) получим:

                                                                                        (3.82)

В свою очередь заметим, что

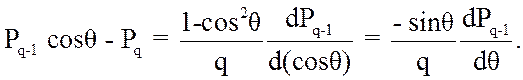
С учетом вышесказанного (3.82) преобразуем к виду:

                                     

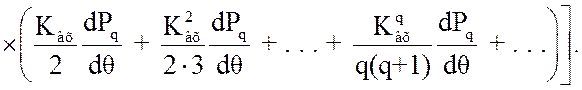                                                                                        (3.83)

                                                                   

Если же НЭМП и полезный сигнал модулированы, то в (3.83) необходимо провести обратную замену, т.е. вместо  записать величину , определяемую в соответствии с (3.71) и (3.73). При это очевидно, что необходимым стало выполнения условия :

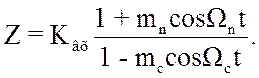                                                            (3.84)

Учитывая тот факт, что большого числа РЭС ГА среднее значение коэффициентов глубины модуляции как полезного, так и помехового сигналов не превышает 0,3, нетрудно установить условие выполнения (3.84):

 или

Если учесть, что фильтры на выходе ЛД не пропускает постоянную составляющую и некоторые компоненты спектра, и, если ширина полосы фильтра , причём ,и , то получим:

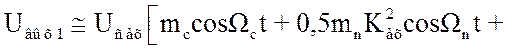
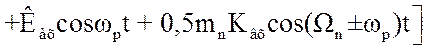                          (3.85)

Часто пользуются критерием устойчивости качественных показателей (УКП), определяемым как выходное отношение сигнал/помеха ко входному, т.е.

                                                                           (3.86)

Определим его для рассматриваемого случая

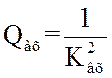
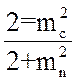                                        (3.87)

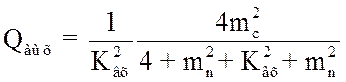                                                (3.88)

Подставляя найденные выражения в (3.86) и считая, что расстройка между несущими частотами не превышает полосу пропускания фильтра, т.е. , имеем:

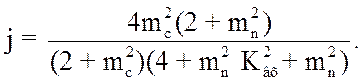                                             (3.89)

С учетом того, что достаточно часто встречается ситуация, когда , (3.89) преобразует к виду:

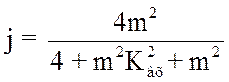                                                                 (3.90)

Если , то несложно получить, что

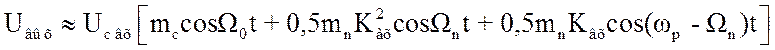                                                                (3.91)