Сущность и особенности проблемы электромагнитного взаимодействия радиоэлектронного оборудования, страница 19

Примеры воздействия помех приведены на рис. 3.6.

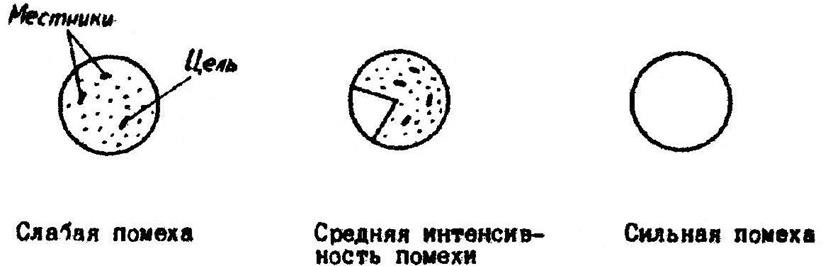
Рис. 3.6. Примеры воздействия помех

К модулированным непрерывным помехам относятся АМ, ЧМ, АЧМ и другие сигналы. Простейшей является АМ помеха:

,

где m – коэффициент модуляции.

При воздействии на ПРМ помеха и сигнал имеют вид:

,

где - моделирующая функция помехи;

,

где - моделирующая функция сигнала.

На выходе детектора образуется суммарное напряжение, огибающая которого равна:

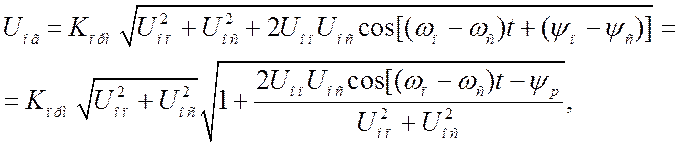                                                                                                           (3.14)

где   ,  - соответственно огибающие функции помехового и полезного сигналов;

         - коэффициент усиления ПРМ.

Если  и , , то на выходе детектора имеем:

,                                                                                                 (3.15)

где     ; ; ;

          ; ;

          .

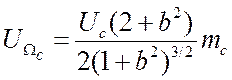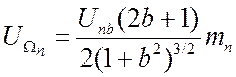Из (3.15) следует, что в данном случае происходит маскировка сигнала помехой, при  сигнал подавляется в детекторе, а отношение с/п при этом равно:

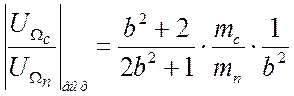.                                                                                                           (3.16)

Так, например, при  и , с/п=.

На экране ИКО модулированные помехи проявляются в виде радиальных и искривленных засвеченных секторах. ЧМ-помехи могут прослушиваться как звуковые сигналы различных типов.

Шумовые помехи – результат их воздействия представлен на рис. 3.7.

Рис. 3.7. Результат воздействия шумовой помехи

3.3. Вероятностные оценки результата воздействия помех

В общем случае вероятность нарушения ЭМС при воздействии всевозможных сочетаний nИП можно записать в виде:

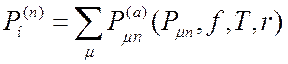,                                                                                                 (3.17)

где      - вероятность -го состояния ЭМО, созданная различными сочетаниями  ИП для -го РП;

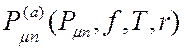           - вероятность нарушения ЭМС при условии осуществления  состояния.

Искомая вероятность нарушения ЭМС находится суммированием вероятностей нарушения для всех ситуаций:

.

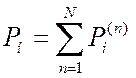Необходимо отметить, что величина 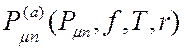 определяется статистическими методами.

Рассмотрим метод решения задачи в случае двух средств. Пусть индекс «1» относится к ИП, а в «2» - к РП. Все исходные данные известны и, кроме этого, известныграницы возможных частот ,  и углов ориентации антенн , ,  и . Значения указанных величин (рабочих частот и углов) считаются случайными и распределены по равномерному закону в указанных границах их определения в силу предположения о некоррелированности их выбора.

Считаем, что  от данного типа ИП для данного РЭС – РП задана. Таким образом,

где    - мощность НЭМП, приведенная по входу ПРМ РЭС, являющегося РП.

В соответствии с [10] искомая вероятность W определяется следующим образом:

                                               

где      - число случайных реализаций вектора  распределенных в области Д его возможных значений;

           - число реализаций вектора R, для которых вычисленное значение  удовлетворяет условию .

Для получения функциональной зависимости вероятности  применяется аналитический метод, основанный на геометрической интерпретации вероятности наступления рассматриваемого события. Его суть заключается в следующем.

Определяем зависимость  мощности НЭМП, приведенной по входу РП (по ОКП), от вектора . Далее вычисляем объем  области Д возможных значений вектора  по формуле:

          (3.18)

и объем  области Д_сД, в пределах которой выполняется соотношение , и который чаще всего определяется методами численного интегрирования на ЭВМ:

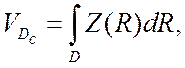          (3.19)

где

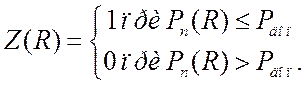          (3.20)

Затем находим искомую вероятность:

.          (3.21)

Вероятность прохождения полезного сигнала через приемник при воздействии внешних импульсных помех и внутренних шумов самого приемника  определяется в виде

          (3.22)

где      - вероятность прохождения сигнала через приемник с учетом внутренних шумов приемника;

           - вероятность совпадения импульсов сигнала и помехи;

           - вероятность интерференционного сбоя импульса сигнала импульсной помехой.