Сущность и особенности проблемы электромагнитного взаимодействия радиоэлектронного оборудования, страница 12

Результат воздействия НЭМП по ПКП при отсутствии полезного сигнала запишем в виде:

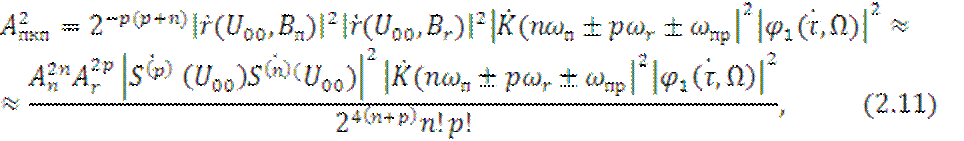
где  

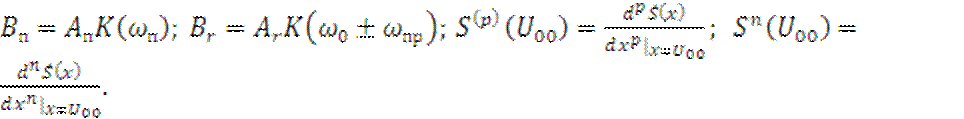
Подставляя (2.9) и (2.11) в (2.8) и решая относительно отношения (2.9), получаем для канала фильтрации, настроенного на сигнал с частотным сдвигом Ω и временем запаздывания  :

,                                                                                               (2.12)

Где  .

Из (2.12) видно, что при постоянной амплитуде сигнала и росте амплитуды колебаний гетеродина восприимчивость к НЭМП, прошедших по ПКП при p ≥ 2, n ≥ 2, уменьшается. Для зеркального канала (n=1, p=1) имеем:

                                                                          (2.13)

Наиболее неблагоприятной является ситуация, когда источники НЭМП распределены равномерно в диапазоне , а спектральная плотность – за пределами ОКП:  при  , p= 2,3 … .

Интегральный показатель ХЧИ. Введём понятие интегральной (энергетической) полосы пропускания ПРМ с учётом ПКП [8,11]:

                                                          (2.14)

где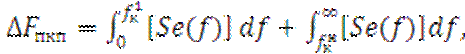  - АЧХ при :

где , - граничные частоты, обусловленные нормами на ШПЧ, и внеполосный спектр излучения [16];  - энергетическая ШПЧ ПРМ.

Мощность НЭМП, прошедших по ПКП , а мощность полезного сигнала, соответствующая чувствительности ПРМ, ограниченного шумами .

С учётом изложенного запишем (2.8) в виде:

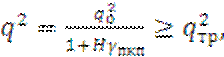                                                          (2.15)

где  – отношение П/Ш; 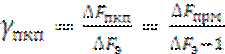  – интегральный параметр ХЧИ по каналам приёма при 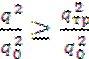. Отношение    , т.е. 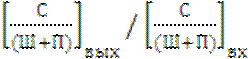 иногда называют коэффициентом помехозащищённости K_пз .

Интегральный показатель ХЧИ с одной стороны определяет, какую долю  по ОКП составляет  по ПКП, а с другой – характеризует степень снижения АЧХ на частотах ПКП по сравнению с АЧХ на рабочих частотах.

Из (2.15) после несложных преобразований получаем:

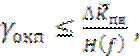                                                    (2.16)

где   – допустимое изменение выходного параметра ХЧИ по каналам приёма, обусловленное воздействие НЭМП.

H(f) численно равен прогнозируемому уровню взаимных помех на частоте f. Очевидно, что H(f) случайная величина, имеющая соответствующие характеристики распределения:

В силу случайного характера H(f), условие (2.16) обеспечивается с некоторой вероятностью p₀,

(2.17)

Используя соотношения[17] при функциональном преобразовании плотности вероятности зависимой величины(2.16), имеем:

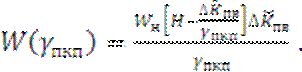                                                        (2.18)

Моделью Флюктуаций амплитуд НЭМП в точке приёма является логарифмическое нормальное распределение [18]:

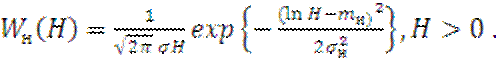                                                                      (2.19)

С учётом (2.18) и (2.19) получим:

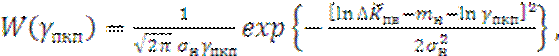                                                                          (2.20)

Распределение (2.20) имеет правостороннюю симметрию, зависящую от  и . Из (2.17) и (2.20) определим значение по заданным  и p₀ из уравнения:

                                                                  (2.21)

где 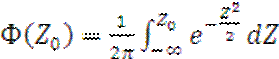 - табличная функция.

Обозначим аргумент функции , численное значение которого определяется из зависимости на рис. 2.2 по заданному значению p₀ , а требования к  определяются в соответствии с [8] (рис. 2.3):

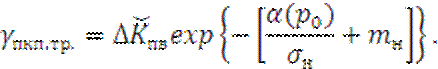
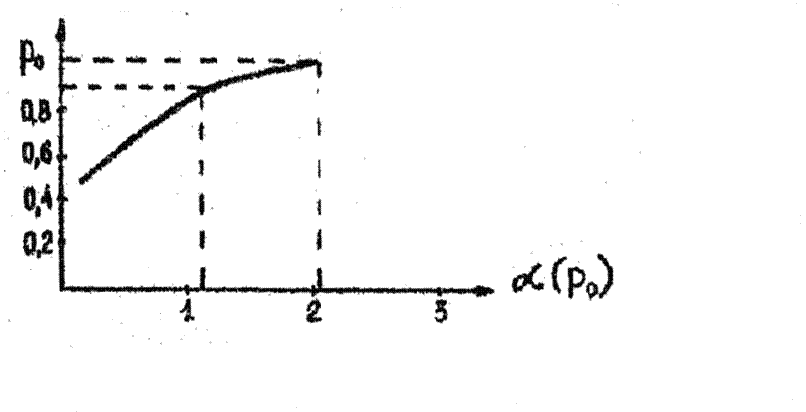
Рис. 2.2. Зависимость  от обобщённого параметра

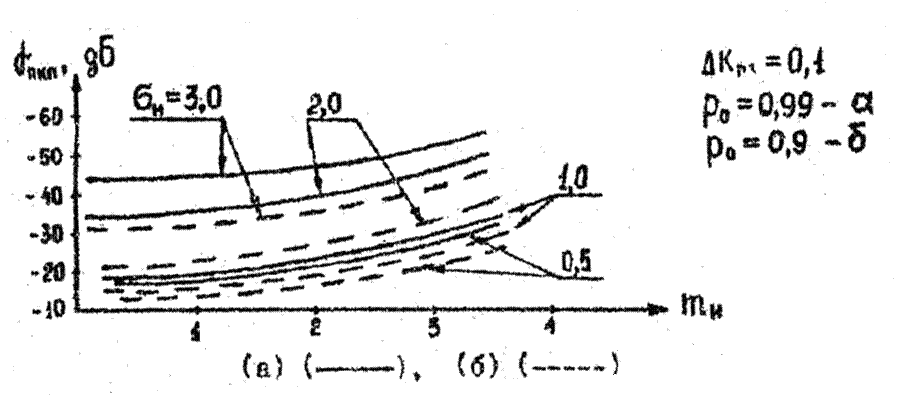
Рис. 2.3. Зависимость  от среднего относительного уровня НЭМП

Значение интегрального показателя ХЧИ по каналам приема позволяет сформулировать требования в области отдельных частот ПКП, вытекающее из эксплуатационных условий функционирования РЭС, наихудшими из которых являются

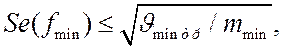
где  - число ПКП.

Оценка ХЧИ по блокированию. Из (2.27) следует, что для

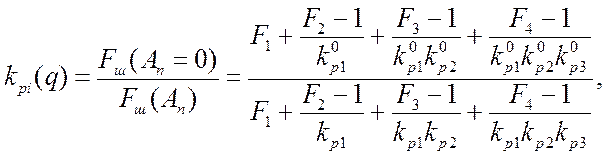                                                                               (2.22)

где  - коэффициент шума -го каскада; ,  - коэффициенты усиления по мощности -го каскада в отсутствии и при наличии НЭМП;  - соответствующий коэффициент шума ПРМ;  = 1,2,3,4 (Ф, УРЧ, Пр, УПЧ).

Выразим коэффициент усиления -го каскада через :

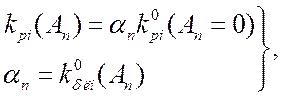                                                           (2.23)

Подставляя (2.23) в (2.22) и разделив числитель дроби на знаменатель, имеем: