Объекты управления и контроля в железнодорожных системах автоматики и телемеханики. Основы теории рельсовых цепей. Классификация систем железнодорожной автоматики и телемеханики, страница 9

где r_oa  – общее активное сопротивление рельсовой петли, Ом/км;

L – общая индуктивность рельсовой петли, Гн/км.

Величина r_oa включает в себя активное сопротивление собственно рель­сов и стыковых соединителей, а L внешнюю и внутреннюю ин­дук­­тивность рельсовой петли и соединителей.

На основании измерений приняты следующие нормативные вели­чи­­ны максимального удельного сопротивления рельсов Z_p для пере­мен­ного тока: частотой 50Гц – 1,0е^j56° Ом/км при стальных штеп­сельных, 0,85е^j60° Ом/км при стальных приварных и 0, 8е^j65° Ом/км при медных приварных соединителях; частотой 75 Гц – 1,07е^j68° Ом/км и частотой 25Гц –  0,5е^j52° Ом/км при медных приварных соединителях.

Отсюда видно, что вид соединителей для РЦ переменного тока су­ще­­ст­венно не влияет на |Z_p|, а применение медных соединителей вы­з­ва­­но только стремлением уменьшить сопротивление рельсов тяго­во­му току. Для РЦ постоянного тока со стальными штепсельными со­е­ди­нителями r = (0,3 – 0,6) Ом/км; со стальными приварными r = (0,1 – 0,2) Ом/км. Отсюда следует, что в рельсовых цепях постоянного тока со­противление рельсов может быть значительно уменьшено приме­не­нием стыковых соединителей с малым сопротивлением.

2.3. Вторичные параметры рельсовой линии

Для любой точки рельсовой линии напряжение и ток можно рас­сматривать как результат распространения двух волн – падающей и от­ра­женной, которые затухают и запаздывают по фазе. Процесс рас­про­странения волн по рельсовой линии характеризуется вторичными или волновыми                     параметрами: коэффициентом распространения вол­ны γ и волновым сопротивлением Z_в.

Коэффициент распространения волны является в общем случае комп­лексной величиной и имеет размерность, обратную длине:

γ = α + jβ  1/км.                                    (2.3)

Действительная часть α характеризует затухание волны, а мнимая часть β, называемая фазовым коэффициентом, определяет степень за­паз­дывания волны по фазе при распространении на единицу длины.

Для рельсовой линии коэффициент распространения волны:

γ= =| | =α+jβ, 1/км;                      (2.4.)

где Z_р – удельное электрическое сопротивление рельсов, Ом/км;

У_и – удельная проводимость изоляции, Ом·км;

φ  –  аргумент сопротивления рельсов;

α = |γ|cos – коэффициент затухания;

β = |γ|sin – фазовый коэффициент.

Бесконечно малый элемент рельсовой линии длиной dx можно приближённо заменить эквивалентной схемой (рис. 2.3):

Рис. 2.3. Эквивалентная схема элемента рельсовой линии

Напряжение и ток в любой точке линии можно рассматривать как результат интерференции двух гармонических волн, распространя­ющихся по линии (рис. 2.4.).

Рис. 2.4. Распространение волн по линии

Волновое сопротивление Z_в  характеризует сопротивление рель­со­вой линии бегущей волне:

 Z_в =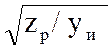=| |,  Ом                           (2.5)

О длине рельсовой линии можно судить по затуханию ( – длина линии), которое испытывает электромагнитная волна при своем распространении. Волновое сопротивление Z_в  и коэффициент распро­стра­нения γ зависят от частоты: с её повышением Z_в  и γ в зна­чи­­тель­ной степени возрастают, аргумент φ  также увеличивается.

В рельсовых цепях постоянного тока (ω = 0) β = 0; α = γ.

Вторичные параметры определяются первичными и последние ока­зывают на них существенное влияние.

2.4. Уравнения и рабочие параметры рельсовой линии

Связь между напряжениями и токами в начале и конце линии устанавливаются при помощи уравнений:

Ů_н  = Ů_кchγl + İ_к Z_вshγl,                                  (2.6)

İ_н  = Ů_к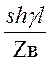+ İ_кchγl.                                        (2.7)

Или  

Ů_н  = АŮ_к + Вİ_к,                                              (2.8)

                                                         

İ_н  = СŮ_к + Dİ_к,                                                (2.9)

где А = D = chγl