Объекты управления и контроля в железнодорожных системах автоматики и телемеханики. Основы теории рельсовых цепей. Классификация систем железнодорожной автоматики и телемеханики, страница 10

коэффициенты рельсового 4-х полюсника                (2.10)

B = Z_вshγl         

C =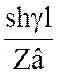

Условия передачи сигналов через рельсовую линию удобно характеризовать рабочими параметрами, к которым относятся:

– сопротивление передачи:

 Z_п  =  = АZ_к  + В = Z_кchγl + Z_вshγl,                      (2.11)

– прямое входное сопротивление:

Z_вх  = = 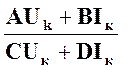=  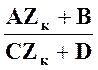= Z_в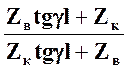.            (2.12)

Если Z_к  = Z_в, то Z_вх  = Z_в.

В режиме к.з. (Z_к  = 0):

Z_{к з}  = Z_вthγl = Z_вth(αl+jβl).                            (2.13)

В режиме х.х. (Z_к  = ∞):

Z_хх  = Z_вcthγl = Z_вcth(αl+jβl).                         (2.14)

Th и cth от комплексного аргумента γl при изменении l изменяют свои модули по волнообразному закону. Поэтому | Z_{к з} | и | Z_хх | также изменяются по волнообразному закону при увеличении l. Для РЦ постоянного тока (γ = L,        βl = 0) в случае R_к  ≠ R_в входные сопротивления R_кз и R_хх изменяются по плавным кривым, соответствующим изменению thαl, cthαl.

2.5. Схемы замещения рельсовых цепей

При расчете, анализе и синтезе рельсовой цепи (РЦ) ее пред­став­ляют в виде схемы замещения  (рис. 2.5), состоящей из каскадного со­е­ди­­нения четырёхполюсников Н, К, РЛ.

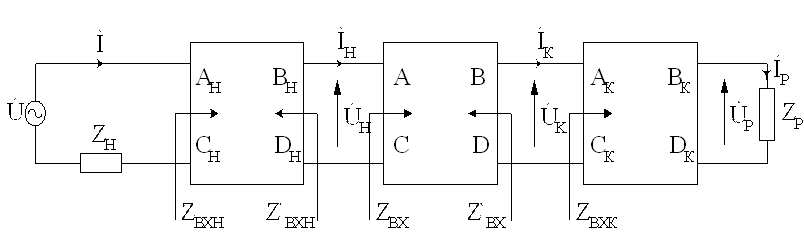
Рис. 2.5. Общая схема замещения сложной РЦ

Четырёхполюсники К и Н за­ме­­щают промежуточную и защит­ную аппаратуру, соответственно, ре­лей­ного и питающего кон­цов. Че­ты­рёхполюсник РЛ замещает только рель­совую линию и назы­ва­ется рель­совым четырёхполюсником. Он мо­­жет замещать рель­со­вую ли­нию во всех основных режимах: нор­маль­­ном, шунтовом и конт­роль­ном. При нормальном режиме этот четы­рёхполюсник харак­теризуют коэффициенты А, В, С, D.

При проектировании и расчетах РЦ обычно идеализируют и рассматривают как линейные и пассивные.

Некоторые простейшие цепи переменного и постоянного тока можно замещать одним четырёхполюсником РЛ, во внешней цепи которого на питающем конце вместо четырёхполюсника Н включено сопротивление Z_н, а на релейном – вместо четырёхполюсника К – сопротивление Z_к (рис. 2.6).

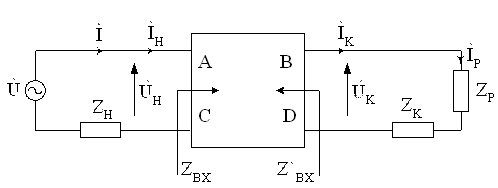
Рис. 2.6. Общая схема замещения простейшей РЦ

При этом Z_н замещает сумму сопротивлений Z₀ и соеди­ни­тель­ных проводов r_сп, а Z_к – сопротивление соединительных проводов на релейном конце r_ср.

Обычно в  теории РЦ  переходят от общей схемы к основной (рис. 2.7), благодаря чему упрощаются расчётные формулы, методы анализа и син­теза схем РЦ.

Рис. 2.7. Основная схема замещения РЦ

Для перехода к основной схеме четырёхполюсник К с нагрузкой Z_р замещают его прямым входным сопротивлением Z_вх.к:

Z_вх.к = 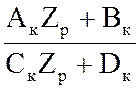,                                        (2.15)

где А_к, В_к, С_к, D_к – коэффициенты четырёхполюсника К.

Четырёхполюсник Н замещают его обратным входным сопротивлением:

Z΄_вх.н = ,                                          (2.16)

где А_н и В_н – коэффициенты четырёхполюсника Н.

Для полученной таким образом основной схемы замещения ток на выходе четырёхполюсника К будет иметь вид:

İ_к = k_тк İ_р,                                              (2.17)

где k_тк = C_кZ_p + D_к – коэффициент снижения тока в четырёхполюснике К.

Этот же ток может быть выражен через сопротивление передачи основной схемы замещения Z_по:

İ_к = 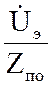,                                               (2.18)

где – напряжение эквивалентного генератора, определяемое как:

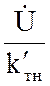=  = ,                                            (2.19)

где – действительное напряжение генератора;

k_тн = А_н – обратный коэффициент тока четырёхполюсника Н.

Согласно общей теории четырёхполюсников сопротивление передачи основной схемы замещения Z_по:

Z_по =  = АZ_вх.к+ В + (CZ_вх.к + D)Z΄_вх.н.                        (2.20)

2.6. Расчёт  и анализ нормального режима