Степень статической неопределимости и выбор основной системы метода сил. Вычисление перемещений в статически неопределимой раме

3.ПРИМЕР  ВЫПОЛНЕНИЯ  РАСЧЁТНОГО  ЗАДАНИЯ

3.1. Исходные данные

         Требуется рассчитать методом сил раму, схема которой представлена на рис. 3.1. По результатам расчёта должны быть построены эпюры внутренних силовых факторов – изгибающих моментов, поперечных и продольных сил от четырёх вариантов воздействий: постоянной распределённой нагрузки q и трёх независимых друг от друга временных воздействий – двух сосредоточенных горизонтальных сил F, изменения температуры Dt на отмеченных штриховыми линиями сторонах стержней и от смещений опорных связей D₍₁₎ , D₍₂₎ , D₍₃₎ . На участке DK построить объемлющую эпюру M_расч и эпюры сил Q_Мрасч и N_Мрасч , соответствующих расчётным моментам. Определить угол поворота  сечения 1 и горизонтальное перемещение узла K отдельно от по-стоянной нагрузки, изменения температуры и смещений связей.

Рис. 3.1

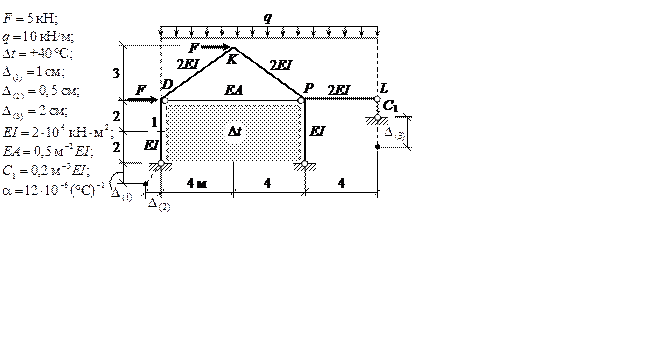
Высоты сечений стоек h_с = 0,3 м. Сечения стержней – симметричные относительно своих главных осей.

Примечание: в индивидуальном расчётном задании студента могут присутствовать параметры, которых нет в исходных данных рассматриваемого примера – относительно них необходимые объяснения приведены далее, например, об угловых упругих связях – на с. 54, по учёту угловых смещений опорных защемлений – на с. 65.

3.2. Степень статической неопределимости

и выбор основной системы метода сил

          Для выявления степени статической неопределимости рамы используем формулу ( 1.1 ),  считая дисками стержень с лома-

ной  осью,  правый  горизонтальный элемент  и  затяжку  ( D = 3 ):

n_st =n_л.с. = – W = – 3D + 3П + 2H + C + C₀ == 3 –

здесь учтена одна припайка в узле P( П = 1), два простых шарнира в узлах D и P ( Н = 2 ), два опорных шарнира и внешняя линейная упругая связь ( С₀ == 5 ).

         По альтернативной формуле ( 1.2 ): n_st  = 3K –  Н== 3

( все шарниры – простые, соединяющие диски попарно ).

X2

         Для выбора основной системы метода сил рассматриваем несколько предварительно намеченных вариантов – они изобра-жены на рис. 3.2, где заданные воздействия условно не показаны.

Рис. 3.2

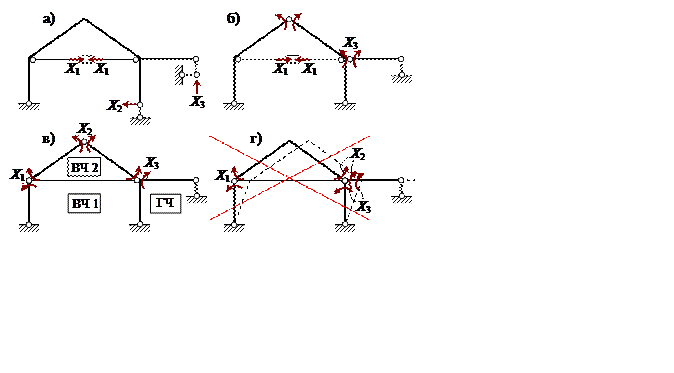
         Сравнение вариантов: вариант «г» отвергается ввиду геометрической  изменяемости  системы  L ;  ОСМС по варианту  «а» хуже других ( см. рекомендацию 2 на с. 9 ), так как получена удалением линейных связей, в том числе опорных. Выполнив кинематический анализ остальных систем, убеждаемся в их геоме-трической неизменяемости. Рациональным является вариант «в» основной системы, поскольку в нём, во-первых, осуществлено удаление только угловых связей, а во-вторых, имеются главная  часть ( ГЧ )  и  две  второстепенных ( ВЧ 1  и  ВЧ 2 ) – все  с достаточно простой структурой J ( см. рекомендации 3 и 4 ).

         Выбранная для расчёта основная система представлена на рис. 3.3.  Она статически определима ( = 3K –  Н== 0

– учтено, что шарниры в узлах D и Р кратные – двойные ).

         На схеме даны одновременно все варианты заданных воздействий; в дальнейшем они будут рассматриваться раздельно.

3.3. Канонические уравнения метода сил. Определение

  и проверка коэффициентов и свободных членов

         Для выбранной основной системы канонические уравнения метода сил имеют следующий вид:

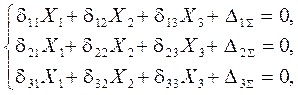
или в матричной форме:

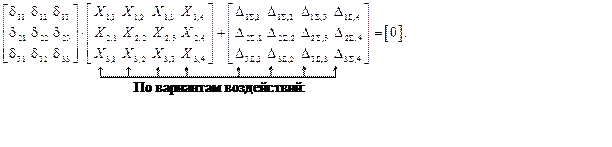
  – вариант 1 – распределенная ( постоянная ) нагрузка q ( const ),

от англ. temporary – временный

  – вариант 2 – две сосредоточенные силы F  ( temp. 1),

  – вариант 3 – изменение температуры Dt      ( temp. 2 ),

  – вариант 4 – смещения опорных связей D_(j) (temp. 3 ).

3.3.1. Единичные состояния основной системы.

Определение и проверка коэффициентов КУМС

         На  рис. 3.4  представлены  схемы  единичных  состояний   основной   системы   ( от   единичных   основных   неизвестных X₁ = 1, …, X₃ = 1 )  и  соответствующие им эпюры изгибающих мо-ментов ( k = 1, 2, 3 – номера единичных состояний). Значения про-дольного усилия в затяжке и реакции упругоподатливой опоры даны на схемах рядом с указанными элементами. Обозначены также продольные силы в стойках, необходимые в расчёте на температурное воздействие, и реакции опор по направлениям заданных смещений связей^*). Размерность реакций и продольных сил от безразмерных моментов X_i = 1 – [ длина ^–1 ].