Степень статической неопределимости и выбор основной системы метода сил. Вычисление перемещений в статически неопределимой раме, страница 3

Rj, i

а)

б)

         Замечание: при наличии в системе

узлов  с  нежёсткими  ( упругими ) угловыми

Рис. 3.5

связями ( рис. 3.5, а )  учитываются их реак-

ции – моменты  R_{j, i} от X_i = 1 ( рис. 3.5, б ).

Х2 = 1

         Коэффициенты при основных неизвестных в канонических уравнениях являются по своей сути перемещениями в ОСМС  по направлениям удалённых лишних связей в единичных состояниях – их смысл иллюстрируется схемами деформаций основной системы, показанными на рис. 3.6.

 

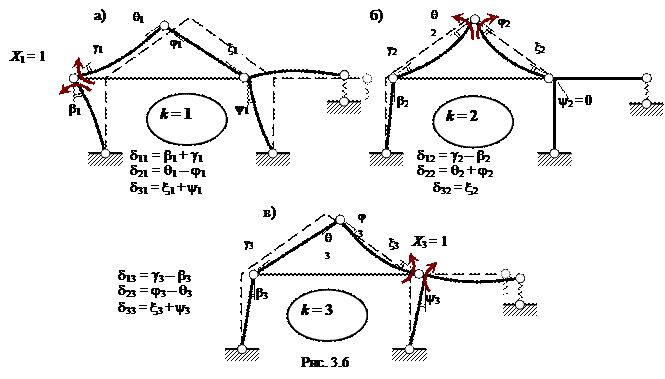
         Единичные перемещения d_ik определяются по формуле       ( 1.13 )  метода  Максвелла – Мора  с  учётом  в  рассматриваемой задаче  деформаций  изгиба  стержней  рамы,  растяжения /сжатия затяжки  и  податливости упругой опоры:

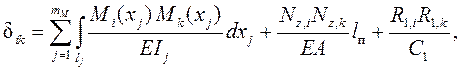
( далее  для  краткости  вместо  M_i (x_j)  и  M_k (x_j)  используются  обозначения M_i  и M_k ).

         Для вычисления интегралов применяется формула Симпсона  или  правило  Верещагина  ( последнее удобно на участках  с простейшими – прямоугольными  или  треугольными – эпюрами,

как во всех единичных состояниях на рис. 3.4 ):

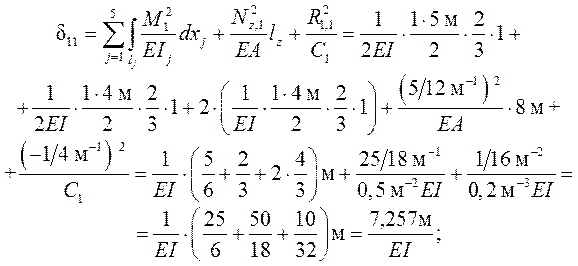
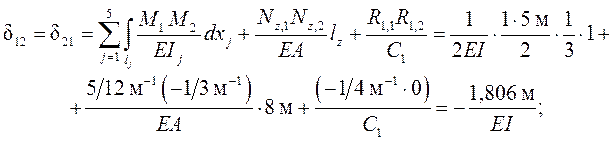
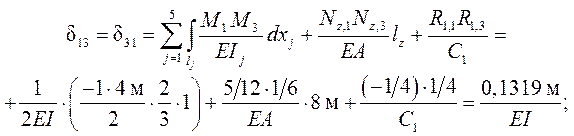
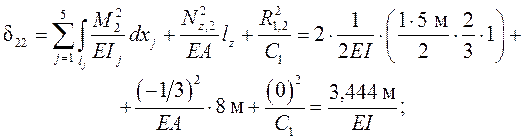
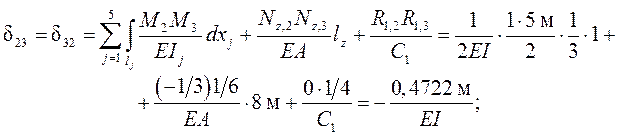
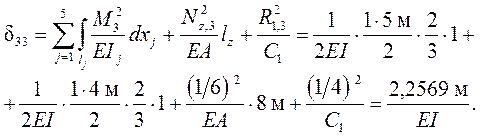
         Для контроля правильности вычисления коэффициентов d_ik производится их универсальная проверка с использованием суммарных  единичных  силовых  факторов  в  основной  системе  ( от  одновременного  действия всех единичных основных неизвестных X₁ = X₂ = X₃ = 1), по условию (1.21). Суммарное единичное со-стояние основной системы показано на рис. 3.7, а, а суммарная единичная эпюра изгибающих моментов M_s – на рис. 3.7, б.

D

Рис. 3.7

         При этом суммарная единичная продольная сила в затяжке N_{z, s} = 1/4,  а  суммарная единичная реакция упругой связи  R_{1, s} = 0. 

         Особо отметим, что моменты M_s ,  а  также  суммарные единичные реакции опор и продольные силы следует определять независимо от ранее найденных M₁ , M₂ , M₃ и соответствующих реакций и продольных сил – это позволяет избежать переноса в M_sи другие суммарные силовые факторы возможных не выявленных ошибок предыдущих расчётов. После этого для дополнительного контроля можно проверить выполнение условия     M_s = M₁ + M₂ + M₃  и аналогично – для реакций и продольных сил.

         Находим обобщённое ( групповое ) сум­марное единичное перемещение d_ss по направлениям всех удалённых угловых связей – сумму взаимных углов поворота сечений у шарниров в узлах D, K и Р:  d_ss = b_s + g_s + q_s + j_s + x_s + y_s ( рис. 3.7, а ). Вычисляем d_ss по формуле, получаемой из ( 1.21 ) удержанием тех же членов, что и в расчёте коэффициентов d_ik :

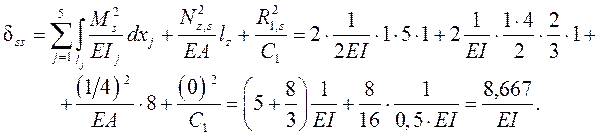
          Полученный результат должен совпасть с суммой всех коэффициентов КУМC:

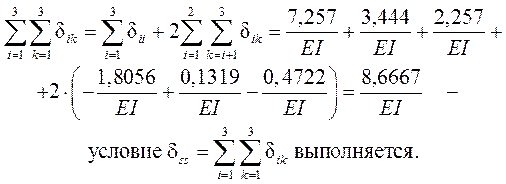
3.3.2. Основнаясистемапризаданныхсиловых,

температурныхикинематическихвоздействиях.

Определение и проверка свободных членов уравнений

          Для нахождения свободных членов канонических уравнений рассматриваются состояния основной системы, соответствующие каждому из четырёх вариантов заданных воздействий. Так как основная система – статически определимая, то усилия в ней возникают только от силовых воздействий ( нагрузок ).

         На рис. 3.8, а, в изображена основная система в двух «грузовых» состояниях – от нагрузок 1‑го ( f = 1 ) и 2‑го ( f = 2 ) вариантов заданных воздействий ( постоянной и первой временной нагрузок ). На рис. 3.8, б, г – соответствующие эпюры изгибающих моментов.

Перемещения в ОСМС по направлениям удаленных лишних связей от силовых воздействий двух первых вариантов ( f = 1, 2 ) определяем также методом Максвелла – Мора – по фор­муле, получаемой как частный случай ( 1.14 ) при учёте тех же видов деформаций элементов рамы, что и в выполненных выше  вычислениях единичных перемещений: