Степень статической неопределимости и выбор основной системы метода сил. Вычисление перемещений в статически неопределимой раме, страница 18

         Следуем рекомендациям по выбору вспомогательных статически определимых систем ( см. с. 41 ), возможно, различных для разных искомых перемещений и обеспечивающих простое вычисление усилий  и  их  локализацию на наименьшем числе не-

лько возможных вариантов вспомогательных   СОС,   в том числе система, которая была  признана рациональной  основной  системой  в  выполненном выше расчёте рамы  методом сил  ( рис. 3.24, б ). Согласно рекомен- дациям, желательно, чтобы  единичное  воздействие  ( в

нулевых расчётных участков.  На  рис. 3.24  представлено  неско-

                                                    а)                           б)

 

                                                    в)                           г)

               

 

Рис. 3.24

                                                                         

рассматриваемой  задаче –

М = 1 в сечении 1 или F = 1 в верхнем узле K ) было бы приложено к главной части ВСОС. Следовательно, главной должна быть левая часть рамы – это имеет место в схемах на рис. 3.24, в и г. Но систему по рис. 3.24, в  рассчитывать сложнее – это трёхшарнирная рама с двумя ломаными стержнями. Поэтому в качестве вспомогательной выбирается система, показанная на рис. 3.24, г. Её удобно использовать при определении обоих перемещений – и углового q₁ , и линейного u_K .  

         На рис. 3.25, а, в  изображены два единичных ( фиктивных )  состояния ВСОС и приведены единичные силовые факторы, необходимые для вычисления перемещений от всех видов воздействий.

 

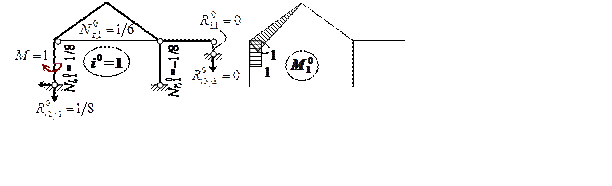
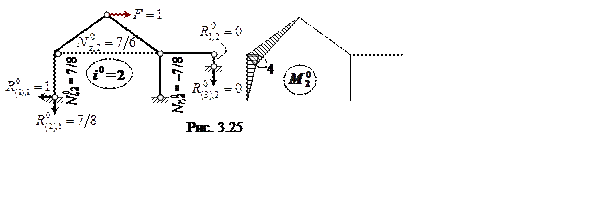Предварительно переименовав искомые перемещения q₁ и u_K  в D_1S и D_2S ( здесь ), в случае силового воздействия  представляем формулу ( 2.2 ) для данной рамы в следующем виде:

тогда

;         

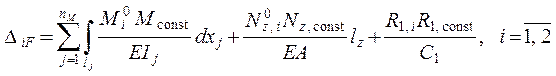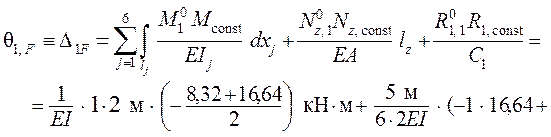
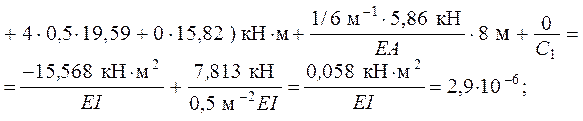
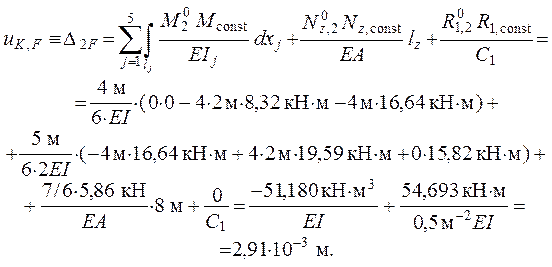
         В выполненных выше вычислениях указаны единицы измерения величин, подставляемых в формулы, – для контроля единиц измерения результата. Далее для краткости это не делается.

         Перемещения от изменения температуры определяем по формуле, получаемой из ( 2.5 ): 

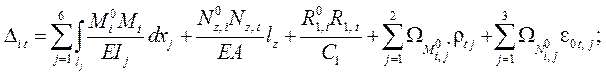
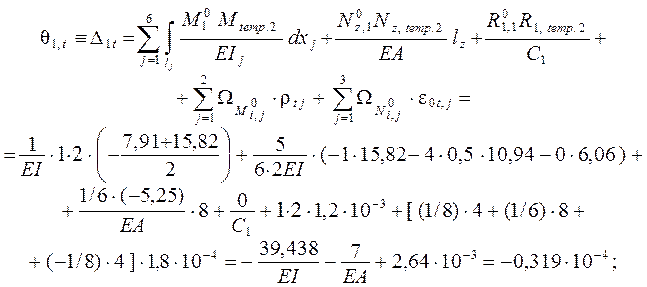
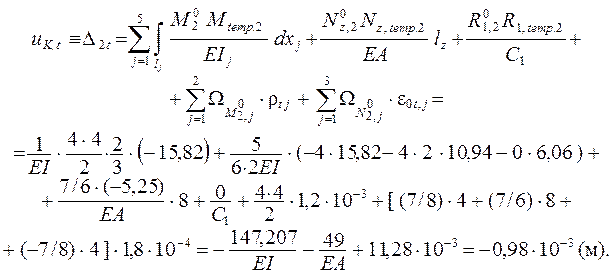
         Перемещения от кинематического воздействия вычисляем на основании формулы ( 2.7 ), дающей в решаемом примере:

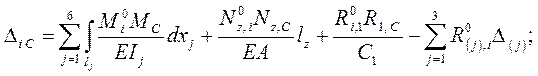
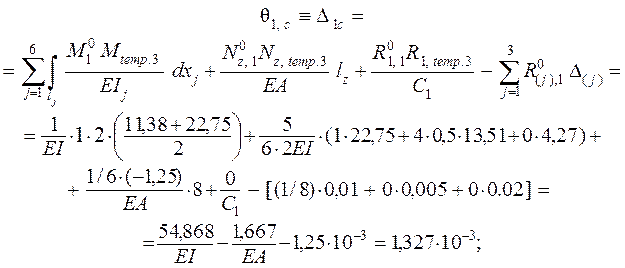
         Для сравнения оценим трудоёмкость расчёта с использованием других вариантов вспомогательной СОС ( рис. 3.26, а, в ).

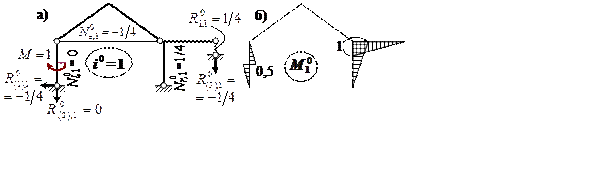
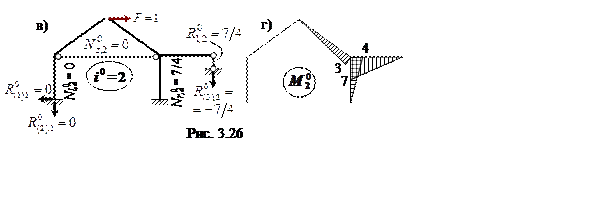
         В обоих случаях получены эпюры более сложные, чем на рис. 3.25. Кроме того, дополнительно придётся учитывать реакцию упругой опоры. Заметим, что при использовании системы по рис. 3.26, в  для расчёта на действие М = 1 получаются в точности такие же усилия, как на рис. 3.26, а, б.

         Обратим внимание на то, что статически определимая система, рациональная в качестве основной системы метода сил  ( рис. 3.26, а ),  не  является  лучшей  для  определения  перемещений.

         В заключение напомним, что можно вычислять перемещения без применения вспомогательной СОС – по форму-лам ( 2.1 ), ( 2.4 ) и ( 2.6 ). Для этого необходимо рассчитать заданную СНС на единичные воздействия М = 1 и F = 1. Если это делать в матричной форме с использованием компьютера, то формально в матрице L_S добавляются 2 столбца усилий в ОСМС от фиктивных единичных «нагрузок». В результате находятся усилия в СНС от М = 1 и F = 1. Этот вариант целесообразен для определения перемещений от температурных и кинематических воздействий.