Для
удобства вычисления интегралов в выражении перемещений Dit строим эпюры rt и e0t
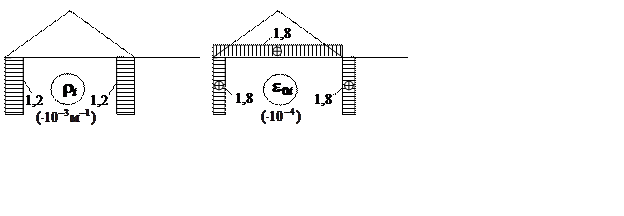
( рис. 3.12 ), причём при построении эпюры rt
используем аналогию с эпюрой изгибающих моментов: знаки не проставляются, а
ординаты откладываются со стороны более «тёплых» волокон элемента
( с алгебраически большим
приращением температуры Dt1 или Dt2 ), т.е. со стороны выпуклости стержня, искривлённого тепловым воздействием. На
эпюре e0t знаки указываются, подобно эпюре продольных сил.
Легко
заметить, что в рассматриваемой задаче все температурные деформации прямо пропорциональны
коэффициенту ЛТР материала a ,
поэтому ординаты эпюр rt и e0t можно было бы
находить с точностью до общего множителя a .
Выполняя «перемножение» единичных эпюр Mi и Ni соответственно
с эпюрами rt и e0t , находим температурные перемещения:
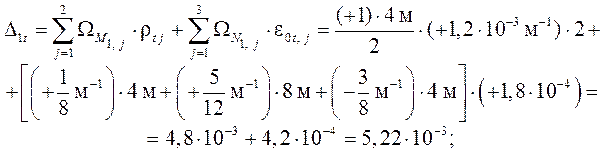
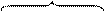
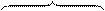
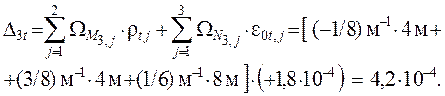
Универсальная проверка найденных
перемещений ( свобод-ных
членов канонических уравнений в случае температурного воздействия ) выполняется также с использованием суммарных
единичных силовых факторов ( см. рис. 3.7 ) – моментов Ms и
про-дольной силы в затяжке Nz, s = 1/4, при этом в левой и правой стойках Nl, s = Nr, s = 0:
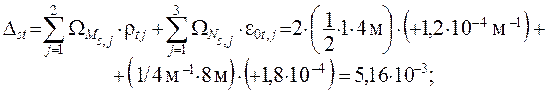
условие 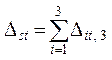 выполняется. выполняется.
|
|
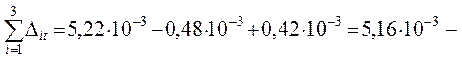
В
последнем варианте воздействий ( f = 4 ) с заданными смещениями опор из
расчётной схемы ОСМС ( рис. 3.12 ) берут-
ся без каких-либо дополнительных
вычислений только значения
компонентов смещений опорных
связей. Нужно лишь следить за
D1c = –bc – gc
D2c = qc – jc
D3c = xc + yc
|
|

тем, чтобы линейные перемещения были описаны
в тех же единицах измерения, которые использовались для размеров рамы в расчёте
реакций смещаемых связей в единичных состояниях ( см. рис. 3.4 ), т.е. в метрах.
Обратим внимание на то, что в статически
определимой основной системе перемещения, вызванные смещениями опор, не
сопровождаются деформациями элементов.
Свободные члены КУМС при кинематическом воздействии –
перемещения в ОСМС – определяются также методом Макс-велла
–
Мора:
.
Значения
реакций R(j), i по направлениям заданных смещений связей приведены на схемах единичных состояний ( рис. 3.4 ).
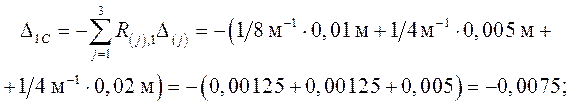

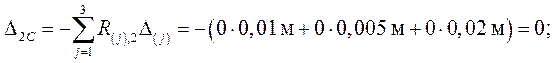
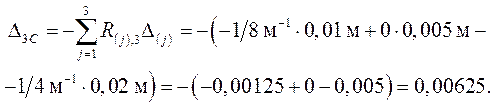

Заметим,
что на напряжённо-деформированное состояние рассматриваемой СНС с
шарнирными
опорами могут оказывать влияние только линейные смещения опорных связей. Повороты
основания
 ( «земли»
) не будут сказываться ни на
( «земли»
) не будут сказываться ни на








перемещениях,
ни
на
усилиях
в
раме

 (
рис.
3.13,
а
).
Но
при
наличии
опорных
(
рис.
3.13,
а
).
Но
при
наличии
опорных









 защемлений
защемлений
угловые
смещения
осно-

вания
(
рис.
3.13,
б
)
должны
учитывать-
ся в расчёте. Например, если бы шар-
нир левой стойки рамы был располо-
положен выше опоры ( рис. 3.13, в ),
то

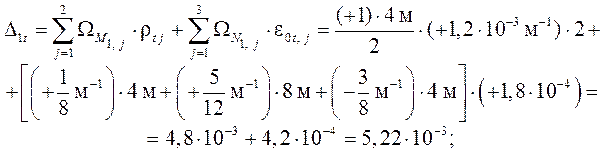
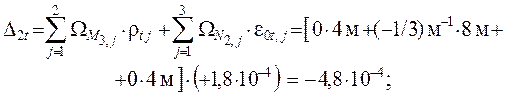
![]()
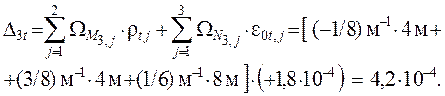
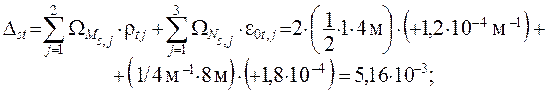
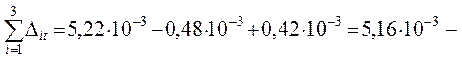

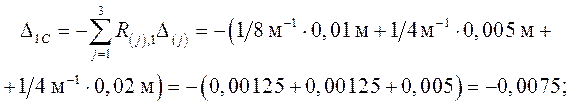
![]()
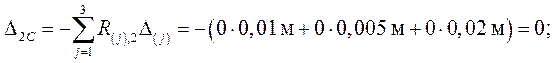
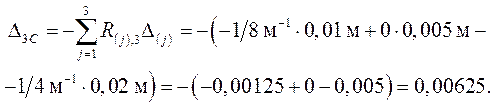
![]()
![]()
 ( «земли»
) не будут сказываться ни на
( «земли»
) не будут сказываться ни на ![]()
![]()
![]() (
рис.
3.13,
а
).
Но
при
наличии
опорных
(
рис.
3.13,
а
).
Но
при
наличии
опорных