Степень статической неопределимости и выбор основной системы метода сил. Вычисление перемещений в статически неопределимой раме, страница 15

         По найденным поперечным силам из условий равновесия узлов, начиная с правого опорного ( рис. 3.17 ), вычисляются про-дольные силы N_{b3, 1} = 0 = N_{e3, 1} , затем N_{b5, 1} и N_{e2, 1} – из уравнений S x_P = 0 и S y_P = 0 для узла Р, остальные – из рассмотрения равновесия узлов K и D ( см. рис.3.1 ) и наклонных элементов KPи KD, к которым приложена нагрузка q. Аналогично определяются по-перечные и продольные силы от остальных вариантов заданных воздействий. Эпюры M, Q и N по всем вариантам представлены на рис. 3.18 и 3.19.

3.4.5. Проверка результатов расчета рамы

        Напоминаем, что в методе сил главной является кинематическая проверка ( см. с. 21 ). Тем не менее, целесообразно начинать с более простой – статической проверки, т.е. контроля выполнения условий равновесия узлов, отсечённых частей и рамы в целом при найденных усилиях в ней, так как если обнаружатся ошибки в статике, выполнять более сложную проверку кинематических условий нет смысла.

Схемы вырезанных внутренних узлов D, K и Р с приложенными к ним усилиями от постоянной нагрузки показаны на рис. 3.20  ( если бы в узлах были приложены внешние силы – узловые нагрузки или реакции внешних связей, их также следовало бы учесть ). Значения и направления изгибающих моментов, продольных и поперечных сил в сечениях, которыми выделены узлы, определяются по построенным эпюрам ( см. рис. 3.18 ).

	K

 

        

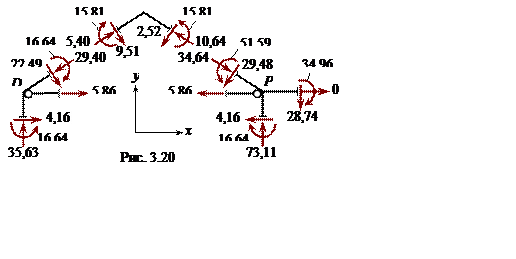
         Подчеркнём, что силовые факторы нужно «считывать» с эпюр, а не брать из компьютерной распечатки, так как проверять следует «конечный продукт» расчёта, а таковым являются именно эпюры M, Q и N. Строго говоря, контролируются усилия, найденные в основной системе. Но если решение правильное, то они должны быть равными искомым усилиям в рассчитываемой СНС. Поэтому на рис. 3.20  и  в  дальнейшем изображаются узлы и части заданной рамы.

         Проверку равновесия начинаем с узла Р:

S m_P = 51,59 – 34,96 – 16,64 = –0,01( относительная погрешность % = –0,019 % );

S x_P  = – 4,16 – 5,86 + = 27,712 – 27,708 =

        = 0,004( +0,014 % );

S y_P  = 73,11 – 28,74 = 73,11 – 73,108 =

           = 0,002( +0,003 % ) – можно считать, что условия равновесия узла Р выполняются с хорошей точностью.

q = 10 кН/м

раму от «земли» сече- нием, проходящим по    стержням бесконечно близко к опорам, пос- ле  приложения  в  се- чениях элементов уси- лий,   взятых   с  эпюр Qconst  и  Nconst ( изгиба- ющие моменты у шар- нирных   опор   равны 0 ),   получаем  схему, представленную   на рис. 3.21.

         Взаимно противоположно направленные одинаковые по абсолютным величинам моменты в узлах D и K попарно точно уравновешивают друг друга. Проверять равновесие сил Q и N в узлах практически бесполезно, так как эти условия ранее были использованы для определения продольных сил по найденным поперечным силам. Значительно более надёжным является контроль равновесия рамы в целом и её отсечённых частей. Отделив

Рис. 3.21

                                 

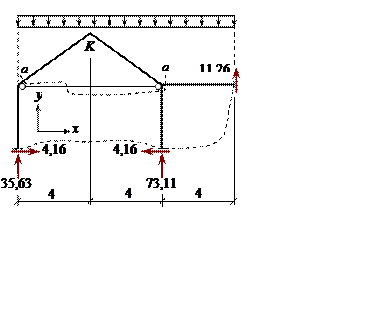
         Проверяем равновесие рамы в целом:        

S x = 4,16 – 4,16 = 0; S y = 35,63 +73,11+11,26 = 120 –120 = 0;

S m_K ==

= 411,64 – 411,64 = 0 – все три уравнения выполняются точно.

         Далее  сечением  а – а  ( рис. 3.21)  отделяем   часть  рамы  и,

q = 10 кН/м

приложив  к  ней  нагрузку  и

выявленные сечением  сило-

K

вые факторы ( рис. 3.22 ), вы-

28,74

22,49

числяем:

4,16

S x = –

5,86