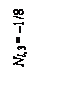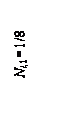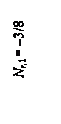Для определения силовых факторов в статически
определимой основной системе как составной раме, имеющей главную и
второстепенные части ( рис. 3.2, в ), используются приёмы расчёта, рассмотренные в 1-й части курса
строительной механики. Например, в первом единичном состоянии ( рис. 3.4, а ) сначала из условия равновесия
левой стойки находится горизонтальная реакция R(2), 1 ; затем рассматривается часть рамы левее шарнира Р (ВЧ1 + ВЧ2), и из
уравнения SmP = 0
определяется R(1), 1 ; наконец, уравнение SmO = 0,
записанное для системы в целом, поз-воляет найти R1, 1 . Заметим, что реакция
правой опоры в последующих расчётах фигурирует в двух качествах – как
реакция R1, i упругой связи и как реакция R(3), i связи, по
направлению которой имеется заданное смещение D(3). Продольная сила в затяжке
оты-скивается из условия равновесия SmK = 0
левой части рамы, отделённой сечением I – I. Далее все внутренние
силовые факторы определяются обычным порядком, даже без вычисления реакций
средней опоры O, показанных на рис. 3.4 пунктирными
линиями. Силовые факторы во 2-м и 3-м единичных состояниях могут отыскиваться
по тому же самому алгоритму. Но имеет смысл обратить внимание на то, что во 2-м
состоянии самоуравновешенное воздействие ( два противоположно направленных момента
X2= 1 ) приложено к одному диску – шарнирному треу-гольнику DKP и
за его пределами никаких усилий не вызывает.
 *) На схеме подлежащие
определению реакции R(j),
i смещаемых связей показы-
*) На схеме подлежащие
определению реакции R(j),
i смещаемых связей показы-
ваются как положительные (т.е. действующие в ту же сторону, что и соответ-
связей Rj, i может быть
любым.
|
|
ствующие смещения D
(j) – см. рис. 3.4). Правило знаков для
реакций упругих




Примечание:
реакции опор
и продольные силы – в м –1.
|
|






















R1, 1 = – R(3), 1 = – 0,25
|
|

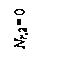










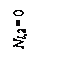













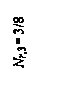
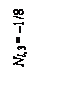










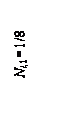
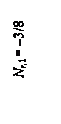

















![]() *) На схеме подлежащие
определению реакции R(j),
i смещаемых связей показы-
*) На схеме подлежащие
определению реакции R(j),
i смещаемых связей показы-![]()