Степень статической неопределимости и выбор основной системы метода сил. Вычисление перемещений в статически неопределимой раме, страница 6

угол поворота q_c следовало бы рассматривать как 4-й компонент D₍₄₎ заданных смещений связей и соответственно в единичных состояниях ОСМС определять опорный момент R_{(4), i} ( рис. 3.13, в ). При выбранных ранее основных неизвестных фрагмент эпюры изгибающих моментов от X₁ = 1 имеет вид, показанный на рис.3.13, г, тогда R_{(4), 1} =       = a/(h – a), где h – высота стойки. В остальных единичных состояниях R_{(4), 2} = R_{(4), 3} = 0. Найденную реакцию R_{(4), 1} нужно умножить на D₍₄₎ и результат учесть при вычислении D_1c.          

         Для проверки найденных D_ic используются суммарные реакции R_{(j), s} ( вычисляемые, как и изгибающие моменты M_s , также независимо от ранее найденных R_{(j), i} ) – см. рис. 3.7, из которого R_{(1), s} = R_{(3), s} = 0;  R_{(2), s} = 1/4. 

условие  выполняется.

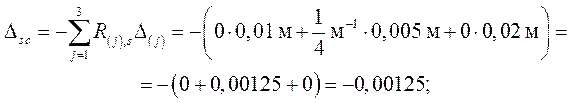
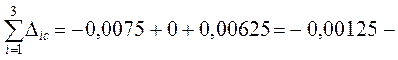
         Используя вычисленные и проверенные коэффициенты и свободные члены, формируем систему канонических уравнений, обращая внимание на то, что все единичные перемещения и    перемещения от заданных силовых воздействий ( в первых двух вариантах,  f = 1, 2 ) определены с точностью до множителя 1/(EI). Величина EI – общий параметр ( масштабная единица измерения жёсткостей, EI = C₀ ), который при записи уравнений в матричной форме может быть вынесен из соответствующих матриц:

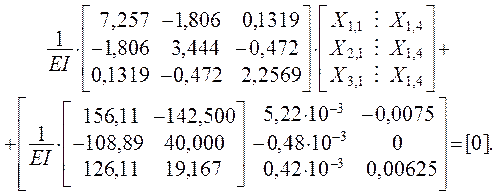
         После умножения на EI получаем систему КУМС в виде

     

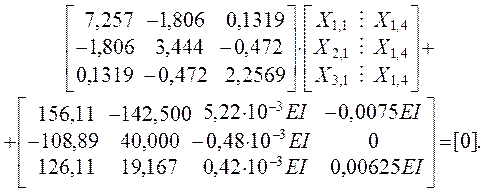
         Очевидно, что определение основных неизвестных в первых двух вариантах воздействий ( силовых ) не требует знания числового значения параметра EI, но для вычисления реакций лишних связей и, следовательно, всех искомых усилий в рассчитываемой СНС от тепловых и кинематических воздействий необходимо использовать EI в числовом выражении. Умножив компоненты последних двух столбцов матрицы L_S свободных членов на EI =( см. п. 3.1 ), получаем:

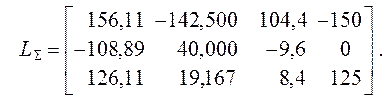
3.4.  Компьютерный расчет рамы в матричной форме

         В разработанной на кафедре строительной механики НГАСУ (Сибстрин) программе MEFOR, предназначенной для расчёта методом сил линейно деформируемых стержневых систем при многовариантных воздействиях силового, кинематического и температурного типов, реализуется вычисление искомых усилий по матричным выражениям ( 1.34 ) и ( 1.36 ). Для  выполнения  расчёта  должны быть составлены и введены в компьютер следующие исходные матрицы:

L  – усилий в упруго деформируемых  элементах ОСМС ( в том числе упругих связях ) в единичных состояниях;

L_F – усилий в упруго деформируемых элементах системы от  заданных нагрузок по вариантам воздействий;

L_t – единичных усилий в элементах с температурными деформациями;

T  – матрица  заданных  приращений  температуры  элементов системы  по вариантам воздействий;

В   – матрица внутренней упругой податливости ОСМС;

B_t  – матрица температурной податливости;

R_D – матрица реакций смещаемых связей от единичных основных неизвестных;

D_c  – матрица заданных кинематическихвоздействий ( смещенийсвязей )  по  вариантам воздействий.

         Для вычисления усилий в специально назначенном наборе, по формулам ( 1.36 ), дополнительно требуются матрицы и  ( см. с. 30 ).

3.4.1. Формирование матриц для расчёта

по программе  MEFOR

         Матрицы  L ,  L_F  и  B  формируются  из  блоков  стандартной структуры в зависимости от количества расчётных сечений на расчётных участках ОСМС c упругими (силовыми) деформациями  ( см. с. 23 ).  Схема  участков  и  сечений,  составленная  по правилам, изложенным на с. 28, приведена на рис. 3.14. Границы расчётных участков назначены:

         – вместахизмененияжёсткостей  сечений;

         – на  границах  грузовых  участков  во всех единичных состояниях ОСМС и в её «грузовых» состояниях (от заданных нагрузок 1-го и 2-го вариантов воздействий); при этом учитывались грузовые участки эпюр изгибающих моментов для элементов рамы с преобладающим изгибом ( стоек, наклонных и правого горизонтального стержней ), а также по одному участку в пре-делах элементов, работающих на растяжение / сжатие, – затяжки и ( условно ) упругой опоры.