Степень статической неопределимости и выбор основной системы метода сил. Вычисление перемещений в статически неопределимой раме, страница 16

34,96

29,40

16,64

16,64

– 5,86 – 4,16 = 23,52 – 23,51=

73,11

= 0,01( + 0,043 % );

4

4

S y = +  

Рис. 3.22

+73,11 – 28,74=

= 108,74 – 108,74 = 0;   

S m_K =16,64=

= 309,08 – 309,07 = 0,01 ( + 0,003 % ) – результат хороший.

         Можно рассмотреть ещё несколько отсечённых частей.

         Кинематическую проверку  выполняем  по  формуле  ( 1.29 ), которая в случае расчёта рамы на постоянную нагрузку записывается в виде

.

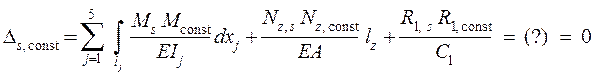         Используя суммарные единичные усилия ( см. с. 56 ) и эпюры, представленные на рис. 3.18, находим

( с погрешностью  – 0,052 % ).

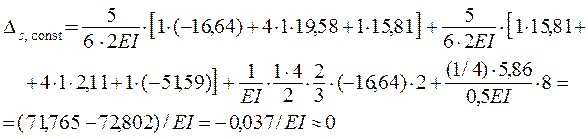
         Аналогично выполняются проверки результатов расчётов при других вариантах заданных воздействий на рассчитываемую раму.

         Не  приводя  здесь  статические  проверки  ( читатель  может самостоятельно убедиться  в  том,  что они выполняются ),  покажем кинематические проверки для вариантов с изменением температуры ( temp. 2 ) и смещениями опор ( temp. 3 ):

,

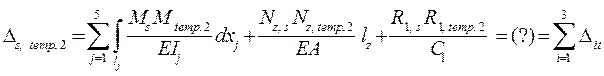где D_it – свободные члены КУМС ( см. с. 63 и 64 ) ;

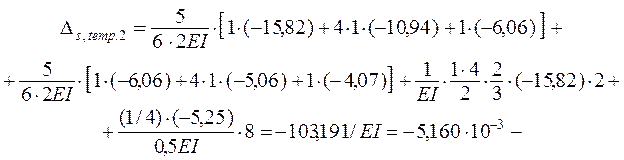точно совпадает с  – (D_1t + D_2t + D_3t ) = – D_st ( см. с. 64 ); 

,

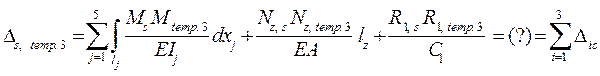где D_iс – см. на с. 65;

( см. с. 66 ).

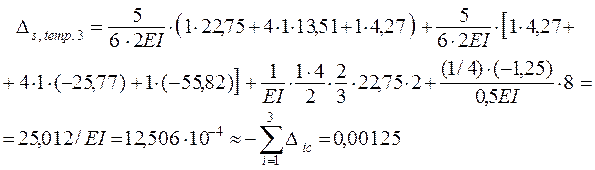
         Замечания:  1. Вместо универсальной кинематической проверки по условию ( 1.29 ) или в дополнение к ней могут выполняться частные проверки по ( 1.30 ).

2. Если использовать формулы ( 1.27 ) и ( 1.28 ), то результаты вычислений по ним с приемлемой вычислительной погрешностью должны быть равными 0.

         Вывод: полная проверка силовых факторов, найденных расчётом статически неопределимой рамы методом сил, свидетельствует о правильности решения задачи.

3.4.6. Построение объемлющей эпюры

изгибающих  моментов

        Расчетные  изгибающие  моменты,  эпюру  которых  ( объемлющую эпюру M_расч ) требуется построить в пределах стержня DK , т.е. на участке 1_М ( рис. 3.14 ), определяются как

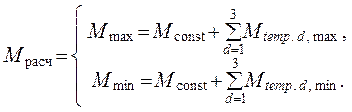
         В дополнение к M_расч находим также соответствующие им поперечные силы Q_Mрасч = dM_расч /dx₁ и продольные силы N_Mрасч .

         Вычисления расчётных моментов M_max и M_min и сопутству-ющих им Q_Mmax , N_Mmax и Q_Mmin , N_Mmin в сечениях, назначенных на участке DK  с  шагом l_DK /4  ( рис. 3.23 ),  удобно  выполнять  в  табличной форме ( табл. 3.1 ). 

        Для  определения  расчётного  момента  M_{j, max}  в  j-м  сечении участка значение момента M_{j, const} от постоянной нагрузки суммируется со всеми положительными моментами от временных воздействий, а при нахождении M_{j, min} – со всеми отрицательными. Поперечные и продольные силы, соответствующие максимальным и минимальным расчётным изгибающим моментам в j-м сечении, вычисляются при тех же сочетаниях воздействий, от которых возникают M_{j, max} и M_{j, min} .

         В рассматриваемом примере при переходе от сечения 2 к е₁ меняются расчётные сочетания воздействий, в результате чего на эпюрах Q_Mрасч  и N_Mрасч  между указанными сечениями наблюдаются скачки ( разрывы ), а на эпюрах M _max и M _min – изломы.

         Так как обязательно учитываемая постоянная нагрузка – равномерно распределённая, то графики M _max и M _min объемлющей эпюры изгибающих моментов состоят из участков парабол 2-й степени, а эпюры соответствующих им Q_Mрасч  и N_Mрасч – кусочно-линейные, с параллельными ( при отсутствии на DK распределённых временных нагрузок ) участками.   

Вычисление расчётных изгибающих моментов и соответствующих им