|
![]()
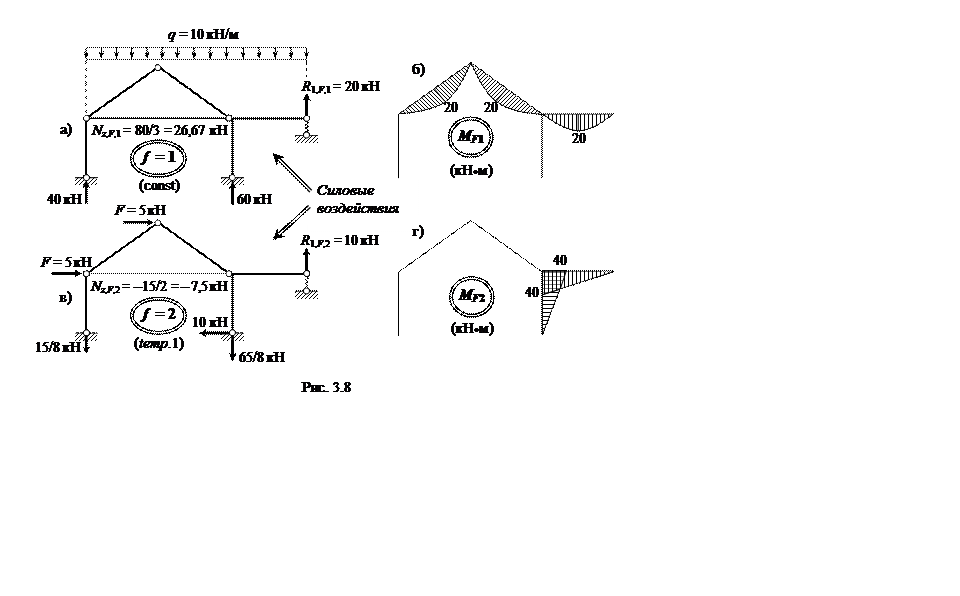
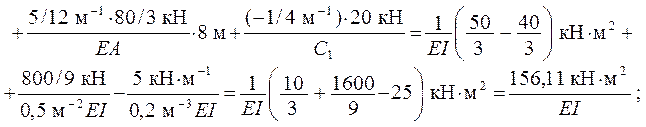
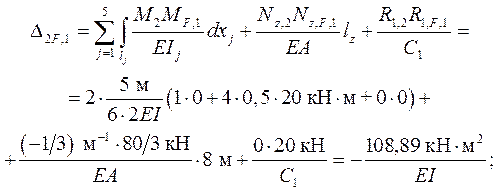
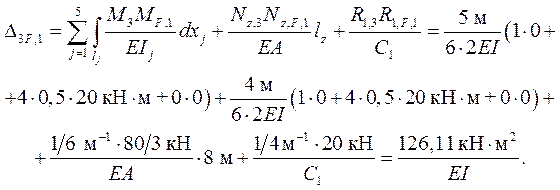
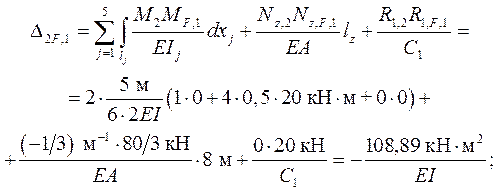
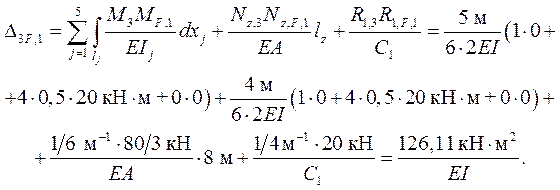
Перемещения DiF, 1 ( i = 1, 2, 3 ) в ОСМС по направлениям ос-новных неизвестных Хi в случае постоянной нагрузки можно ис-
толковать по схеме деформаций, показанной на рис. 3.9:
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
|
|
|


![]()
![]() Проверка правиль-
Проверка правиль-
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ности вычисленных «гру-
ности вычисленных «гру-
![]()
|
|
![]()
![]()
|
( 1.23 ), которое для рас-
![]()
![]()
![]()
![]()
![]()
![]() считываемой рамы в слу-
считываемой рамы в слу-
|
требует определения об-
общённого ( суммарного ) перемещения DsF, 1 по формуле
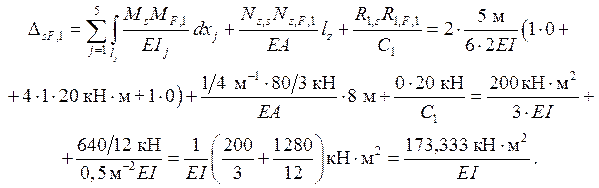
Сопоставляем полученный результат с суммой ранее найденных свободных членов канонических уравнений
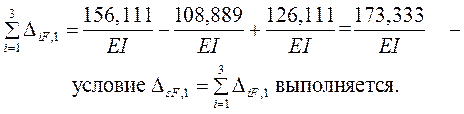
|
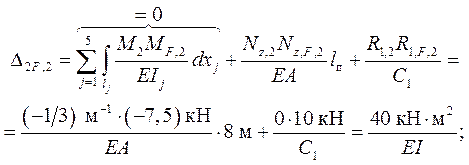
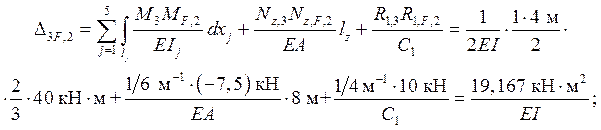
Проверка:
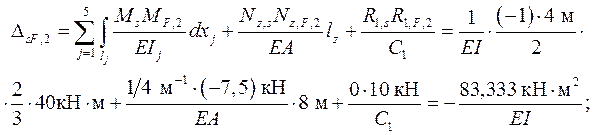
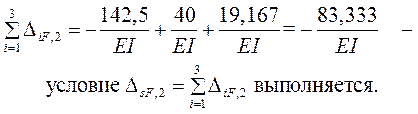
|
|
тогда 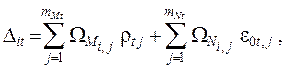
где ![]() – площади эпюр Mi и Ni на j-ом участке.
– площади эпюр Mi и Ni на j-ом участке.
На рис. 3.10 представлены расчётные данные о температурном режиме элементов рамы. Приращения температур Dt1 описываются на нижних волокнах горизонтальных стержней и на правых волокнах вертикальных элементов, а Dt2 – соответственно на верхних и левых. При вычислении составляющих приращений температуры элемента ( равномерной*) Dt0 и неравномерной Dtnr ) по формулам, воспроизведённым на рис. 3.10, обязательно учитываются знаки Dt1 и Dt2 .

Кривизна оси левой стойки:
rt, l
=![]() (0,3 м) =
(0,3 м) = ![]() м
–1 ;
м
–1 ;
 для правой стойки rt, r =
для правой стойки rt, r =
= – rt, l
= – ![]() м –1.
м –1.
Кривизну оси затяж-
ки, не работающей на из-
гиб, можно не определять.
Относительные про-
дольные температурные
деформации стоек и за-
|
![]()
|
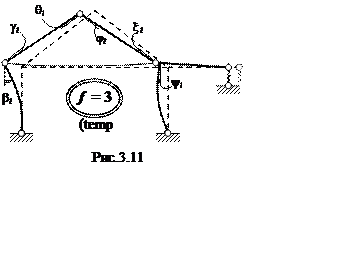
Перемещения Dit ( i = 1, 2, 3 ) в ОСМС по направлениям основных неизвестных Хi в случае изменения температуры можно истолковать по схеме деформаций, показанной на рис. 3.11:
D1t = bt + gt ; D2t = – qt – jt ; D3t = xt + yt .
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.