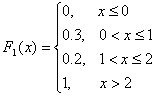
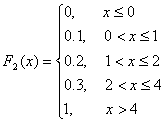 Если
«да», то найти МХ.
Если
«да», то найти МХ.
8. Случайная величина Х распределена по нормальному закону с параметрами
а = –1 и ![]() = 2. Найти вероятность попадания в интервал [1.25 ,
2.55]. Записать плотность распределения f(x) и
функцию распределения F(x).
= 2. Найти вероятность попадания в интервал [1.25 ,
2.55]. Записать плотность распределения f(x) и
функцию распределения F(x).
9. Найти а , коэффициент корреляции
двумерной случайной величины (X,Y), если f(x,y) = а х 2 sin у , 0 ![]() х
х![]() 1 , 0
1 , 0![]() у
у ![]() π .
π .
8 вариант
1.Есть 5 одинаковых партий изделий. Каждая партия состоит из 4 изделий первого сорта и 1 изделия второго сорта. Из каждой партии наудачу берут изделие. Найти вероятность того, что среди выбранных хотя бы 3 изделия первого сорта.
2. В театральной кассе к некоторому моменту времени осталось n билетов в театр эстрады и 8 билетов в драматический театр. Найти n , если вероятность того, что два билета будут приобретены очередным покупателем в театр эстрады,
равна ![]() .
.
3. В урне 20 шаров, из них 5 черных. Наудачу взято 3 шара. Найти вероятность того, что среди выбранных хотя бы 1 черный шар.
4. Группа состоит из 2 стрелков. Если каждый стрелок сделает по 1 выстрелу, то: а) вероятность совместного промаха равна 0.12, б) вероятность того, что в цель попадет только 1 стрелок, равна 0.46. Найти вероятность попадания в цель каждым стрелком.
5. Партия состоит из 8 изделий первого сорта и 32 изделий второго сорта. Наудачу взято5 из них. Найти вероятность того, что среди них ровно 4 одного сорта.
6. Пусть n- число независимых испытаний, р- вероятность появления события А в отдельном испытании, k- число наступлений события А за n испытаний:
а)n=б00, р=0.4. Найти P(k>210).
б) Найти ε, если р=![]() , n=5929, P
, n=5929, P![]()
7. Дискретная случайная величина Х задана рядом распределения
|
x1 |
2 |
4 |
6 |
8 |
|
|
0.4 |
0.3 |
0.2 |
0.1 |
Построить
график функции распределения F (х), вычислить ![]() X.
X.
8. Случайная величина Х задана функцией распределения:
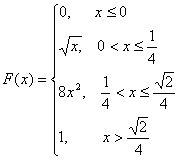 Построить графики f(x) и F(x),
найти σX
Построить графики f(x) и F(x),
найти σX
9. Найти коэффициент корреляции двумерной случайной величины (X,Y),
заданной матрицей
|
х\у |
1 |
2 |
4 |
|
I |
0.1 |
0.3 |
0.1 |
|
3 |
0.2 |
0.1 |
0.2 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.