Экзаменационные билеты по дисциплине "Теория вероятностей и математическая статистика", страница 11

заданной матрицей

у\х	10	20	30
1'	0.3	0.2	0.1
2	0.2	0.1	0.1

17 вариант

1. В каждой из 4 одинаковых партий деталей по 15 деталей первого сорта и по 5 деталей второго сорта. Из каждой партии берут по 1 детали. Какова веро­ятность взять по 2 детали каждого сорта?

2. Производят 3 выстрела по одной мишени. Вероятность попадания при каждом выстреле равна 0.5. Найти вероятность того, что в результате этих выстрелов произойдет только 1 попадание.

3. В классе 20 мальчиков и 10 девочек. На каждый из 3 вопросов, заданных учителем, ответили по 1 ученику. Найти вероятность того, что среди отвечавших было 2 мальчика и 1 девочка.

4. В первой урне 1 белый и 2 черных шара, во второй- 100 белых и 100 черных шаров, Из второй урны переложили в первую 1 шар, а затем из первой урны вынули наудачу 1 шар. Какова вероятность того, что вынутый шар ранее находился во второй урне, если известно, что он белый?

5. Всхожесть семян данного сорта растений оценивается с вероятностью, равной 0.8. Какова вероятность тоги, что из 5 посеянных семян взойдут не менее 4?

6.Пусть n- число независимых испытаний, р- вероятность появления события А в отдельном испытании, k- число наступлений события А за n испытаний:

    a)n=400, р= . Найти Р(k<160).

    б) Найти, если n=525, р=0.7, Р

7.  Определить, является ли функция 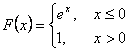 функцией распределения.

    Если "да", то найти Р (-2 Х1), построить графики f(x) и F (х).

 8. Дискретная случайная величина Х задана рядом

-2	-1	0	1	2
0.1	0.2	0.3	0.3	?

Определить закон распределения с.в. Y = |Х|, найти Y.

9. Найти а, коэффициент корреляции двумерной случайной величины (Х,У),

   если f (х,у) = а х cos 2y, 0x2, 0y

18 вариант

1.Имеются 3 одинаковые на вид урны. В первой - 2 белых и 3: черных шара, во второй - 4 белых и 1черный, в третьей - 3 белых шара. Найти вероятность того, что шар, вынутый из наудачу выбранной урны, будет белым.