Экзаменационные билеты по дисциплине "Теория вероятностей и математическая статистика", страница 2

    Определить значение параметра а, плотность вероятности и ее значения в точках   и . Найти МХ и вероятность того ,что с.в.Х примет значение в интервале [, 2].

8. Случайная величина Х задана рядом распределения

Найти функцию распределения с.b.Z == 2 x³, σ Z .

9. Найти а , коэффициент корреляции двумерной случайной величины (X,Y), если f(x,y)= а  ,

3 вариант

1. Наудачу выбрано натуральное число, не превосходящее 20. Какова вероятность того, что 20 нацело делится на это число?

2. В партии из 10 изделий-2 бракованных. Наудачу выбирают 5 изделий. Определить вероятность того, что среди них 1 бракованное.

3. Студент знает 50 из 60 вопросов программы. Найти вероятность того, что студент знает 2 вопроса, содержащиеся в экзаменационном билете.

4. Из урны, содержащей 3 белых и 7 черных шаров, один шар неизвестного цвета утерян. Какова вероятность извлечь наудачу из урны шар белого цвета?

5. Вероятность того, что покупателю потребуется обувь 41 размера, равна 0.2. Найти вероятность того, что из 5 покупателей одному потребуется обувь этого размера.

6. Пусть n-число независимых испытаний, р- вероятность появления события А в отдельном испытании, k- число наступлений события А за n испытаний:

    а) n=400, р==0.5. Найти вероятность Р (178<k<201).

    б) Найти ε, если р=, n=400, Р=0.95.

7. Плотность распределения c.в.X: f(x) Ae, λ>0, х≥0. Найти коэффициент А, функцию распределения F(X), вычислить вероятность попадания с.в.Х в интервал (0,).

8. Определить , является ли функция F(x) функцией распределения с.в.Х :

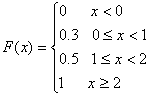                       Записать закон распределения с.в.Х . Найти  Х .

9.Найти а , коэффициент корреляции двумерной случайной величины (X,Y), если f(x,y) = а х³ у³, 0  х  1 , 1 у2.

4 вариант

1. Брошены 3 монеты. Найти вероятность того, что выпадут 2 "герба".

2. Из 10 карточек с буквами А, Д,, А, Б, А, Д, В, Г, Д, А наудачу выбираются 3. Какова вероятность того, что из этих карточек можно сложить слово "два"?

3. Стрелок стреляет 3 раза по удаляющейся цели. Вероятность попадания при первом выстреле - 0.8, при втором - 0.7 и при третьем - 0.6. Какова вероятность хотя бы одного попадания?

4. 60% школьников - девочки. 80% девочек и 75% мальчиков имеют билеты в театр. В учительскую принесли потерянный кем-то билет. Какова вероятность того, что этот билет принадлежит девочке?.