Гидравлика: Лабораторный практикум, страница 9

Закон сохранения массы для установившегося потока несжи­маемой жидкости в канале с непроницаемыми стенками для условий сплошности (неразрывности) течения сводится к закону постоянства расхода вдоль канала и выражается уравнением объемного расхода (рис. 3.1):

,                 (3.1)

где  – средние скорости потока в сечениях 1 и 2;  – площади сечения 1 и 2.

Из уравнения следует, что средние по сечению скорости в потоке несжимаемой жидкости обратно пропорциональны площадям сечений:

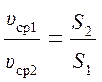.          (3.2)

Средней по нормальному сечению скоростью потока () называется одинаковая для всех точек сечения скорость, обеспечивающая действительный расход через это сечение:

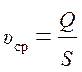.             (3.3)

Эпюры скоростей в нормальном сечении потока в трубе для ламинарного и турбулентного течений при одинаковом расходе, а также эпюра средней по сечению скорости приведены на рис.3.2. Нормальное сечение – это сечение, нормальное в каждой точке к скорости потока (живое сечение).

3.2. Уравнение Бернулли для потока реальной жидкости

Закон сохранения (изменения) энергии для установившегося потока несжимаемой вязкой жидкости в поле сил земного притяжения выражается уравнением Бернулли (рис. 3.3):

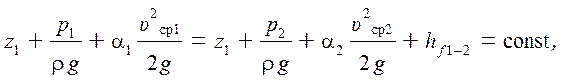     (3.4)

где z₁ и z₂ – геометрические высоты центров тяжести сечений 1 и 2; p₁ и p₂ – давление в центрах тяжести сечений 1 и 2; a₁ и a₂ – безразмерные коэффициенты неравномерности распределения скоростей в сечениях 1 и 2;  – средние скорости потока в сечениях 1и 2.

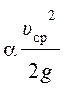Члены уравнения Бернулли в приведенной форме имеют линейную размерность (м)и при геометрической трактовке уравнения их определяют как высоты, напоры: z – геометрическая высота, или геометрический напор;  – пьезометрическая высота,  – скоростная высота, или скоростной напор.

Трехчлен 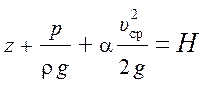 называется полным напором. Из-за неравномерного распределения скоростей по сечению трубы (рис. 3.2) этот трехчлен выражает среднее значение полного напора в сечении.

При энергетической трактовке уравнения Бернулли (3.4) члены уравнения представляют собой различные формы удельной механической энергии жидкости, приходящейся на единицу ее веса (размерность ):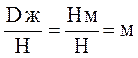

z – удельная потенциальная энергия положения;

 – удельная потенциальная энергия давления (возможная работа сил давления, отнесенная к единице веса жидкости);

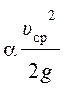 – удельная кинетическая энергия потока в данном сечении;

z+ – удельная потенциальная энергия;

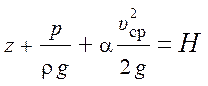 – полная удельная механическая энергия движущейся жидкости в данном сечении (среднее по сечению значение полной удельной энергии);

_f1-2 – суммарные потери полной удельной энергии (полного напора) на участке трубопровода между сечениями 1 и 2.

Из уравнения Бернулли (3.4) следует:

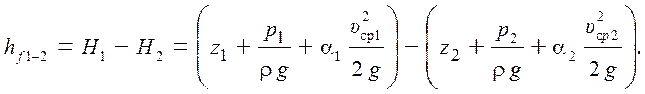(3.5)

Потери удельной механической энергии потока (гидравлические потери) обусловлены работой сил внутреннего трения и вихреобразованием. Они складываются из потерь напора (энергии) на трение по длине трубопровода  и потерь в местных сопротивлениях, расположенных на рассматриваемом участке, :

.                              (3.6)

При ламинарном течении потери напора на трение по длине возрастают пропорционально скорости (расходу) в первой степени (формула Пуазейля), при переходе к турбулентному течению имеется некоторый скачок сопротивления, и затем происходит нарастание  по кривой, близкой к параболе второй степени

(рис. 3.4).

Вихревые потери, связанные с отрывом потока и вихреобразованием в самом местном сопротивлении или за ним, при турбулентном и ламинарном течениях пропорциональны скорости во второй степени.

Безразмерный коэффициент a(коэффициент Кориолиса), учитывающий неравномерность распределение скоростей по сечению потока, представляет собой отношение действительной кинетической энергии потока, вычисленной по местным скоростям, к кинетической энергии, вычисленной по средней скорости:

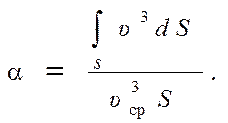(3.7)

Для обычного распределения скоростей (рис. 3.2) коэффициент  всегда больше единицы, а при равномерном распределении скоростей равен единице. Для ламинарного потока с параболическим распределением скоростей 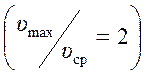 коэффициент