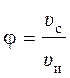 ,
,
т. е. коэффициент скорости j есть отношение действительной скорости истечения υск скорости идеальной жидкости υи .
Опыты показывают, что скорость в ядре струи равна идеальной, а наружные слои движутся медленнее, так как заторможены взаимодействием со стенкой. Поэтому действительная скорость истечения всегда несколько меньше идеальной. Расход жидкости, проходящий через отверстие, определится как произведение действительной скорости на фактическую площадь сечения струи:
![]() .
.
Принимая во внимание, что
![]() и
и ![]() ,
,
будем иметь
![]() .
.
Произведение коэффициентов e и j принято обозначать буквой m и называть коэффициентом расхода, т.е.
m = ej.
Тогда
![]() ,
,
отсюда
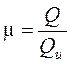 ,
,
т. е. коэффициент расхода есть отношение действительного расхода к тому расходу Qи, который имел бы место при отсутствии сжатия струи и сопротивления. Величина Qи не является расходом при истечении идеальной жидкости, т. к. сжатие струи будет иметь место и при отсутствии гидравлических потерь.
Действительный расход
всегда меньше теоретического вследствие влияния двух факторов: сжатия струи и
сопротивления. Значения коэффициентов истечения e, j, m и ![]() зависят от размеров отверстия,
условий подтока к нему жидкости и числа Рейнольдса.
зависят от размеров отверстия,
условий подтока к нему жидкости и числа Рейнольдса.
 |
При истечении через квадратное отверстие (рис. 7.2, б) струя постепенно превращается в крест с тонкими прозрачными ребрами, ориентированными нормально к сторонам квадрата. Вытекающая через треугольное отверстие (рис. 7.2, в) струя постепенно принимает форму звезды с ребрами, перпендикулярными сторонам треугольника.
 |
Коэффициент сжатия e определяется в результате измерений струи в сжатом сечении. Диаметр сжатого сечения можно определить с помощью специального приспособления (рис. 7.3), которое представляет собой кольцо с четырьмя микрометрическими винтами. Приспособление устанавливается на кронштейне так, что струя проходит внутри кольца.
Подводя острия винтов к поверхности струи, замеряют диаметр струи в двух взаимно перпендикулярных направлениях d1 и d2.
Коэффициент сжатия определяют по выражению
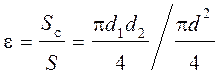 , или
, или 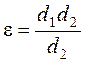 .
.
Для нахождения коэффициента расхода m действительный расход вычисляют объемным способом:
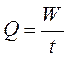 ,
,
где W – объем вытекающей жидкости;
t –- время наполнения объема W по секундомеру
Теоретический расход находят по формуле
![]() ,
,
где S – площадь отверстия.
Полный напор с учетом скорости подхода υ0
![]() .
.
Скорость υ0 можно определить по формуле
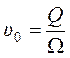 ,
,
где W – площадь сечения резервуара.
Коэффициент расхода определится по зависимости
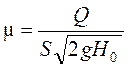 .
.
Для определения коэффициента скорости j производят измерения координат струи с помощью координатной сетки, закрепленной на кронштейне (рис. 7.4).
Располагая начало координат (x = y = 0) в центре тяжести сжатого сечения, для точки А будем иметь следующие соотношения:
x= υс t, 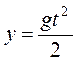 ,
,
где t – время движения частицы жидкости от сжатого сечения до рассматриваемого.
Выразив время t из первого соотношения и подставив его в выражение для y, получим
y =![]() , или
, или 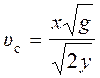 .
.
Коэффициент скорости равен
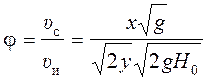 ,
,
или
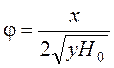 .
.
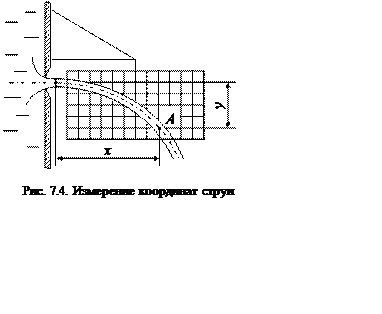 Зная коэффициент скорости, можно определить
коэффициент сопротивления:
Зная коэффициент скорости, можно определить
коэффициент сопротивления:
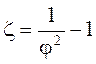 .
.
Таким образом, известны коэффициенты истечения e, j и m для вычисления площади, скорости и расхода струи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.