Гидравлика: Лабораторный практикум, страница 10

= 2 и не зависит от числа Rе. При турбулентном течении распределение скоростей по сечению более равномерное, а нарастание скорости у стенки более крутое, чем при ламинарном течении. В связи с этим коэффициент  при турбулентном течении значительно меньше . Он является функцией числаRеи уменьшается с увеличением последнего от 1,13 при Rе = Re_кр до 1,025 при Rе = 3·10⁶. В большинстве случаев при турбулентном течении можно принимать = 1.

Уменьшение среднего значения полной удельной энергии жидкости вдоль потока (полного напора), отнесенное к единице длины рассматриваемого участка трубы, называется гидравлическим уклоном (рис. 3.3):

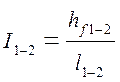.                                   (3.8)

Для потока реальной жидкости уравнение Бернулли (3.4) является уравнением баланса энергии с учетом потерь. Оно применимо не только для жидкостей, но и для газов при условии, что скорость их движения значительно меньше скорости звука.

3.3. Геометрическая интерпретация уравнения Бернулли

Графически уравнение Бернулли (3.4) можно представить в виде диаграммы (рис. 3.3), где показано изменение высот (напоров) вдоль потока. Линия изменения пьезометрических высот называется пьезометрической линией, ее можно рассматривать как геометрическое место уровней в пьезометрах, установленных вдоль трубы. Из уравнения расхода и уравнения Бернулли следует, что если площадь поперечного сечения потока уменьшается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если поток (труба) расширяется, то скорость уменьшается, а давление возрастает, что и отражается на форме пьезометрической линии. Если жидкость течет по трубе постоянного сечения, то из условия неразрывности потока скорость течения и кинетическая энергия жидкости остаются неизменными вдоль трубы. В этом случае на преодоление сопротивления движению жидкости расходуется энергия давления. Таким образом, пьезометрическая высота может изменяться как в результате изменения площадей сечений потока, так и из-за возникновения потерь энергии.

Линия полного напора для потока вязкой жидкости показывает характер уменьшения полной удельной механической энергии (полного напора) вдоль трубы вследствие потерь энергии [см. формулу (3.5)]. Потери представлены на диаграмме высотой , которая неуклонно возрастает вдоль потока. Интенсивность понижения линии полного напора на рассматриваемом участке трубы характеризуется гидравлическим уклоном [формула (3.8)].

Вертикальные отрезки (высоты), заключенные между линией полного напора и пьезометрической линией, дают величину скоростного напора (удельной кинетической энергии) в различных сечениях (в принятом масштабе).

Для определения взаимного высотного расположения отдельных точек, уровней гидросистемы используется горизонтальная плоскость, проведенная на произвольной высоте и называемая плоскостью сравнения. Положение плоскости выбирается из практических соображений (например, нулевая отметка на измерительной шкале, свободная поверхность бассейна и т. п.). Вертикальное расстояние рассматриваемой точки от плоскости сравнения (0–0) называется геометрической высотой z. Взаимное высотное расположение двух точек 1 и 2 определяется как разность геометрических высот этих точек:. Как видно из схемы (рис. 3.3), для любых двух сечений можно составить равенство суммы высот в форме уравнения (3.4), которое является геометрической интерпретацией уравнения Бернулли и поясняет его энергетический смысл.

3.4. Трубки пьезометрического и полного напоров

Пьезометрический (статический) напор в сечении потока жидкости измеряется пьезометром. Пьезометр (рис. 3.5) представляет собой тонкую вертикальную стеклянную трубку (а), верхний конец которой открыт в атмосферу, а нижний нормальный срез проходит через мерную точку потока и ориентирован параллельно скорости потока Высота подъема жидкости в пьезометре (пьезометрическая высота)

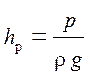,                                        (3.9)

где p – избыточное давление в точке присоединения пьезометра.