 .
.
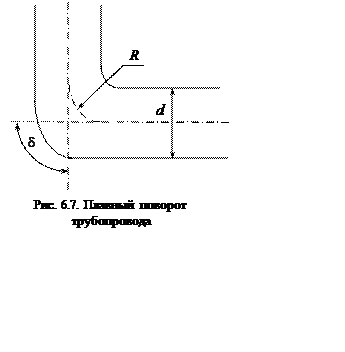 При плавном повороте трубы (закругленное колено,
отвод) вихреобразования уменьшаются, и потери напора будут значительно
меньше (рис. 6.7). Это уменьшение будет тем больше, чем больше относительный
радиус кривизны R/d и при достаточно большом его значении вихреобразования
ликвидируются полностью. Коэффициент сопротивления отвода зависит от
относительного радиуса кривизны, угла поворота, коэффициента гидравлического
сопротивления
При плавном повороте трубы (закругленное колено,
отвод) вихреобразования уменьшаются, и потери напора будут значительно
меньше (рис. 6.7). Это уменьшение будет тем больше, чем больше относительный
радиус кривизны R/d и при достаточно большом его значении вихреобразования
ликвидируются полностью. Коэффициент сопротивления отвода зависит от
относительного радиуса кривизны, угла поворота, коэффициента гидравлического
сопротивления ![]() ,
а так же от формы поперечного сечения трубы. Для отводов кругового сечения с
,
а так же от формы поперечного сечения трубы. Для отводов кругового сечения с ![]() коэффициент
сопротивления может быть определен по формуле:
коэффициент
сопротивления может быть определен по формуле:
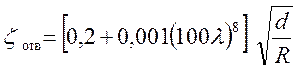 .
.
При повороте на любой угол ![]() можно
использовать зависимость
можно
использовать зависимость
![]() ,
,
где k – коэффициент смягчения, в первом приближении
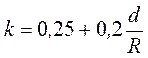 .
.
Другие более сложные случаи местных сопротивлений представляют собой соединения или комбинации рассмотренных простейших сопротивлений.
Законы истечения жидкости через отверстия и насадки имеют большое практическое значение, поскольку они встречаются при решении многих технических задач.
В процессе истечения потенциальная энергия жидкости частично превращается в кинетическую энергию струи и частично затрачивается на преодоление гидравлических сопротивлений. Задача состоит в определении скорости истечения жидкости, ее расхода и гидравлических потерь при заданных условиях или необходимых условий для получения заданного расхода и скорости истечения.
Рассмотрим истечение жидкости из сосуда неограниченной емкости в атмосферу через отверстие в боковой стенке при постоянном напоре Н и следующих условиях (рис. 7.1):
- отверстие мало (d/H < 0,1), что позволяет принять постоянство напора для любой точки отверстия (d – диаметр отверстия);
- стенка либо тонка, либо имеет острую кромку, что исключает потери на трение по длине;
- отверстие достаточно удалено от дна и боковых стенок, что обеспечивает свободное и симметричное подтекание струек жидкости к отверстию со всех сторон.
Частицы жидкости, обтекая кромку отверстия, движутся по криволинейным траекториям, что приводит к возникновению центробежных сил, направленных к оси и сжимающих струю до минимального диаметра dс на расстоянии примерно (0,5÷1,0)d от внутренней поверхности стенок сосуда. В этом сечении давление в струе становится равным давлению окружающей среды (pа). За сжатым сечением струя практически не расширяется. Отношение площади сечения сжатой струи Scк площади отверстия S называется коэффициентом сжатия струи
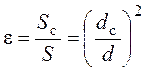 .
.![]()
Таким образом, степень сжатия оценивается коэффициентом сжатия струи.
Для определения скорости истечения запишем уравнение Бернулли для движения жидкости от свободной поверхности ее в резервуаре (рис. 7.1, сеч. 0–0):
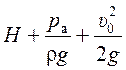 ,
,
и до сжатого сечения струи (рис. 7.1, сеч. 1–1):
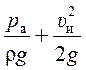 ,
,
где pa – атмосферное давление; υо – скорость движения жидкости; υи – скорость истечения идеальной жидкости; H – напор жидкости.
Приравнивая оба уравнения, получим
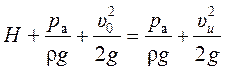 , или
, или 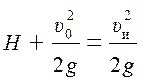 .
.
Выражение в левой части этого уравнения является полным напором над центром отверстия с учетом скорости движения жидкости в сосуде υо и обозначается через H0:
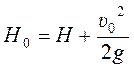 , тогда
, тогда 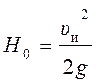 .
.
Откуда скорость истечения идеальной жидкости равна
![]() .
.
Теоретический расход жидкости, т. е. расход, который имел бы место при отсутствии сжатия струи и сопротивления,
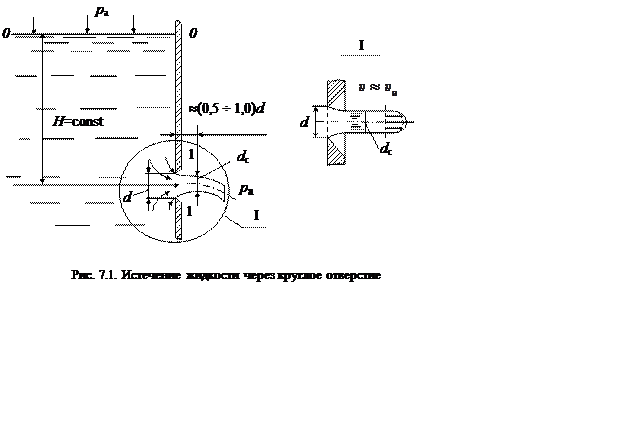 |
Уравнение Бернулли для выделенных сечений в случае истечения реальной жидкости при условии равномерного распределения скоростей в сосуде и струе (aо = a1 = 1) запишется следующим образом:
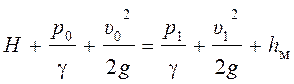 .
.
Принимая во внимание, что pо = p1 = pа, υ1 = υс, 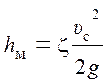 (местные
потери, обусловленные сопротивлением при истечении из отверстия с острой
кромкой), будем иметь
(местные
потери, обусловленные сопротивлением при истечении из отверстия с острой
кромкой), будем иметь
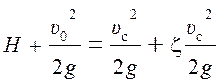 ,
,
или
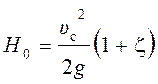 .
.
Отсюда получаем выражение для средней скорости в сжатом сечении струи:
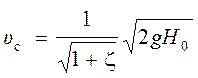 .
.
Выражение 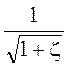 обозначается через j и называется
коэффициентом скорости, т. е.
обозначается через j и называется
коэффициентом скорости, т. е.
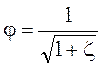 ,
,
откуда 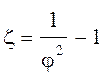 .
.
Тогда
![]() ,
,
или ![]() , откуда
, откуда
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.