Гидравлика: Лабораторный практикум, страница 16

Рассмотрим случай, когда трубопровод резко расширяется от диаметра d₁ до диаметра d₂ (рис. 6.1). Поток, выходящий из узкой трубы, не сразу заполняет все поперечное сечение широкой трубы, жидкость в месте расширения отрывается от стенок и дальше движется в виде струи, отделенной от остальной жидкости поверхностью раздела. Поверхность раздела неустойчива, на ней возникают вихри, в результате чего транзитная струя перемешивается с окружающей жидкостью. Струя постепенно расширяется, пока, наконец, на некотором расстоянии от начала расширения не заполнит все сечение широкой трубы. В кольцевом пространстве между струей и стенками трубы жидкость находится в вихревом движении. Это вихревое движение организуется за счет сил трения на поверхности раздела между основным потоком и застойной зоной. Затрата энергии на преодоление сил трения и создания вихревого движения приводит к значительным потерям напора.

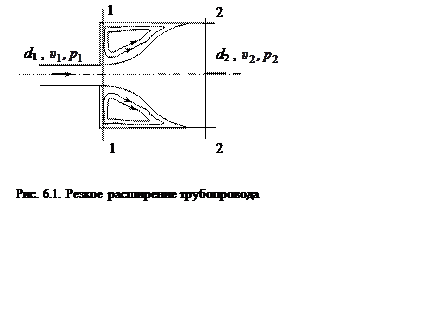Пользуясь уравнением энергии (уравнением Бернулли) и уравнением количества движения, найдем величину этих потерь. Обозначим средние скорости потока в сечениях 1–1 и 2–2 через  и , а давления через p₁ и p₂ . Давление на торцевой стенке, как показывает опыт, практически равно давлению на выходе из узкой трубы, т. е. p₁ .Считая распределение скоростей по сечениям равномерным (), соединим уравнением Бернулли оба сечения:

,

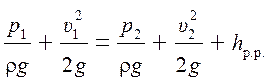или

,

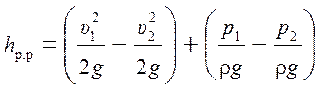где  – потеря напора на резкое расширение потока.

Разность давлений определим, пользуясь уравнением количества движения, которое приложим к объему жидкости, заключенному между сечениями 1–1 и 2–2:

,                      (6.3)

где  – плотность жидкости; Q – объемный расход жидкости;

T₀ – проекция на направление движения внешней силы трения, действующей со стороны стенок трубы на рассматриваемый объем жидкости; G – проекция веса объема жидкости на направление движения, G=0; P – сумма проекций сил гидравлического давления P₁ и P₂ , действующих соответственно на торцевые сечения 1–1 и 2–2 выделенного отсека транзитной струи.

Так как длина участка потока между сечениями 1–1 и 2–2 невелика, то силой T₀ можно пренебречь.

Величину P можно представить в виде уравнения

P = P₁ – P₂ = S₂ (p₁ –p₂),                    (6.4)

где S₂ – площадь сечения второй трубы.

Учитывая (6.4), уравнение (6.3) можно записать в виде

,

откуда, имея в виду, что ,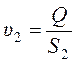

получаем

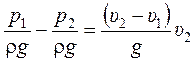.                       (6.5)

Подставляем (6.5) в (6.2) и получаем

,

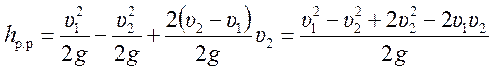или окончательно

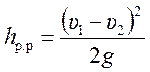,                              (6.6)

где разность  называют потерянной скоростью.

Выражение (6.6) называется формулой Борда. Согласно этой формуле потеря напора при резком расширении равняется скоростному напору от потерянной скорости. Выражение (6.6) можно привести к другому виду.

Вынесем за скобки , тогда получим

.

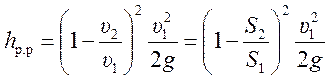Обозначая

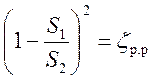,                         (6.7)

имеем

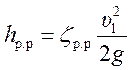.                            (6.8)

Вынося за скобки , получаем

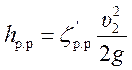,                            (6.9)

где

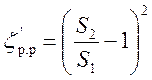.                         (6.10)

Коэффициенты  называются коэффициентами сопротивления при резком расширении потока.

Потеря напора, получающаяся при резком выходе потока из трубы в резервуар больших размеров, называется потерей на выход. В этом частном случае, когда S₂ значительно больше S₁ получаем, что , и, следовательно, потеря на выходе будет

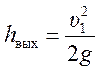,                                  (6.11)

т. е. теряется весь скоростной напор, вся кинетическая энергия, которой обладает жидкость.

6.2. Постепенное расширение трубопровода

Постепенно расширяющаяся труба называется диффузором. При постепенном расширении трубы потери напора значительно уменьшаются. При течении жидкости в диффузоре (рис. 6.2) скорость постепенно уменьшается, а давление увеличивается. Кинетическая энергия частиц движущейся жидкости уменьшается как вдоль диффузора, так и в направлении от оси к стенкам. Слои жидкости у стенок обладают столь малой кинетической энергией, что не могут преодолеть нарастающего давления, останавливаются и начинают двигаться обратно. При столкновении основного потока с обратными течениями возникают отрыв потока от стенок и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла конусности диффузора, а вместе с этим растут и потери на вихреобразования.