Гидравлика: Лабораторный практикум, страница 12

4.2. Число Рейнольдса

Режим движения жидкости в трубе зависит от величины безразмерного числа, которое учитывает основные факторы, определяющие движение жидкости в трубе: среднюю скорость течения  , диаметр трубы , плотность жидкости  и ее абсолютную вязкость. Это число называется числом Рейнольдса и имеет вид

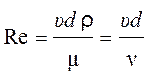 ,                                (4.1)

где  – кинематический коэффициент вязкости.

Значение числа Рейнольдса, при котором происходит переход от одного режима движения жидкости к другому, называется критическим числом Рейнольдса . Для круглых труб в обычных условиях для критического числа Рейнольдса принимают значение , отвечающее переходу движения из турбулентного в ламинарное. При переходе движения из ламинарного в турбулентное критическое число Рейнольдса имеет большую величину. Однако при  ламинарный режим оказывается крайне неустойчивым, и малейшее возмущение приводит к бурной турбулизации потока. Поэтому на практике за критическую величину числа Рейнольдса принимают значение . Величина критического числа Рейнольдса в сильной степени зависит от случайных возмущений потока в трубе: тряски, неровностей поверхности стенок трубы, поперечных конвективных токов, вызванных нагревом, плохообтекаемых предметов в потоке; изменения формы и размеров канала и т. д.

При  режим движения является ламинарным, при  – турбулентным.

Величина  в числе Рейнольдса может быть заменена любым характерным линейным параметром, связанным с условиями течения или обтекания.

С физической точки зрения число Рейнольдса можно рассматривать как отношение сил инерции к силам трения. Сила инерции движущегося элемента жидкости равна

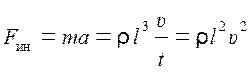,                      (4.2)

где  – характерный линейный размер элемента жидкости.

Сила трения рассматриваемого элемента жидкости может быть определена по формуле

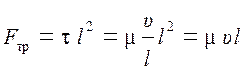.                       (4.3)

Отношение силы инерции к силе трения будет равно

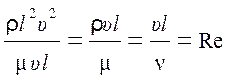.                 (4.4)

Таким образом, число Рейнольдса характеризует относительную роль сил вязкости. Чем меньше число Рейнольдса, тем большую роль играют силы вязкости в движении жидкости. Чем больше число Рейнольдса, тем больше влияние сил инерции в потоке по сравнению с силами вязкости.

4.3. Особенности ламинарного и турбулентного
движения жидкости

Одновременно с переходом ламинарного движения в турбулентное изменяется характер распределения скоростей по сечению трубы, а также величина гидравлических сопротивлений (рис.4.3).

При ламинарном течении распределение скоростей по сечению имеет параболический характер: скорости непосредственно на стенках равны нулю, а при удалении от стенок – непрерывно и весьма плавно возрастают, достигая максимума на оси трубы
(рис. 4.3, а).

При турбулентном течении закон распределения скоростей сложнее: в пределах большей части сечения скорости лишь незначительно меньше максимальной скорости на оси, но зато вблизи стенок величина скорости резко падает (рис. 4.3, б).

Более равномерное распределение скоростей по сечению при турбулентном течении объясняется наличием турбулентного перемешивания. Благодаря этому перемешиванию частицы с большими скоростями в центре потока и с меньшими скоростями на его периферии, непрерывно сталкиваясь, выравнивают свои скорости. У самой стенки турбулентное перемешивание парализуется наличием твердых границ, и поэтому там наблюдается значительно более быстрое падение скорости.

Если пропускать жидкость в трубе с различной скоростью, то зависимость гидравлического сопротивления от скорости будет иметь вид, представленный на рис.3.4. До значения скорости, равного критическому, т. е. до момента перехода от ламинарного движения к турбулентному потери напора изменяются прямо пропорционально скорости. При скоростях движения, больших критической, вид зависимости потерь на трение меняется и потери напора становятся пропорциональными квадрату скорости.