X = j - g×sin a ; Y = 0 ; Z = - g×cos a.
Подставляя эти выражения в уравнение равновесия (2.1), получаем
dp = ![]() [(j - g×sin a)dx
- g×cos a dz],
[(j - g×sin a)dx
- g×cos a dz],
а после интегрирования
p = ![]() (j
- g×sin a)×x
-
(j
- g×sin a)×x
- ![]() g×cos a×z
+ C, (2.2)
g×cos a×z
+ C, (2.2)
где С – постоянная интегрирования, определяемая из граничных условий на свободной поверхности при x = 0, z = z0 и p = p0.
После подстановки граничных условий получаем закон распределения давления:
p
= р0+![]() (j - g×sin a)×x +
(j - g×sin a)×x +![]() ×g×cos a×(z0 - z).
(2.3)
×g×cos a×(z0 - z).
(2.3)
Так как на поверхности уровня давление одинаково в любой ее точке, полагая в уравнении (2.2) p = const, получаем уравнение поверхностей уровня
![]() ( j - g×sin a)×x -
( j - g×sin a)×x - ![]() ×g×cos a×z + C1 = 0. (2.4)
×g×cos a×z + C1 = 0. (2.4)
 |
Подставляя в формулу (2.4) граничные условия x = 0 и z = z0, находим
C1 = ![]() ×g×z0×cos a.
×g×z0×cos a.
Уравнение свободной поверхности имеет вид
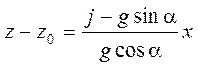 ,
(2.5)
,
(2.5)
где 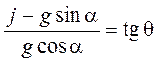 .
.
2.3. Равновесие жидкости в цилиндрическом сосуде,
равномерно вращающемся вокруг вертикальной оси
Равновесие жидкости в сосуде, вращающемся вокруг вертикальной оси, реализуется лишь при постоянной угловой скорости вращения w = const (рис. 2.2).
По истечении достаточного времени после начала вращения жидкость приобретает ту же скорость вращения, что и сосуд, а свободная поверхность ее видоизменяется: в центральной части уровень жидкости понизится, у стенок – повысится и вся свободная поверхность станет некоторой поверхностью вращения (рис.2.2, а). На жидкость в этом случае будут действовать две массовые силы: сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w²r.
При проецировании на оси координат равнодействующей массовых сил (рси.2.2, б) получим выражения
X = w2 r cos a= w2 ×x ; Y = w2 ×r×sin a = w2 ×y ; Z = – g.
dp = ![]() (w2xdx +w2ydy – gdz),
(w2xdx +w2ydy – gdz),
или
dp = ![]() (w2rdr – g dz).
(w2rdr – g dz).
 |
![]()
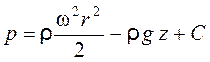 . (2.6)
. (2.6)
Подставляя в уравнение (2.6) граничные условия r = 0, z = z0 и p = p0, находим постоянную интегрирования
C = р0 + ρg×z0.
Тогда закон распределения давления можно выразить формулой
![]() ,
(2.7)
,
(2.7)
т. е. в этом случае также справедлив линейный закон распределения давления по глубине. Изменение давления по радиусу подчиняется параболическому закону. Полагая p = const, из выражения (2.6) получим уравнение поверхностей уровня:
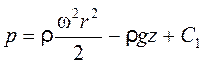 . (2.8)
. (2.8)
Эти поверхности уровня представляют собой параболоиды вращения. Одним из таких параболоидов является свободная поверхность жидкости.
Так как в вершине параболоида свободной поверхности r
= 0, z = z0, C1 = ![]() g×z0 ,то
уравнение свободной поверхности примет вид
g×z0 ,то
уравнение свободной поверхности примет вид
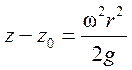 . (2.9)
. (2.9)
Зависимость
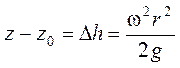 (2.10)
(2.10)
при постоянном
радиусе (r= const) устанавливает
связь между величиной возвышения ![]() любой точки, расположенной на
свободной поверхности над точкой, лежащей на оси вращения, и угловой скоростью w. Она позволяет
определить число оборотов цилиндра, если известно превышение
любой точки, расположенной на
свободной поверхности над точкой, лежащей на оси вращения, и угловой скоростью w. Она позволяет
определить число оборотов цилиндра, если известно превышение ![]() , что и
используется при конструировании жидкостных тахометров, с помощью которых
измеряется число оборотов вала.
, что и
используется при конструировании жидкостных тахометров, с помощью которых
измеряется число оборотов вала.
Угловая скорость определяется по выражению
w = 2×p×n/ 60 = p×n/ 30.
Отсюда формула для определения числа оборотов:
n= 30× w/ p.
Из выражения (2.10) следует
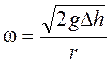 .
.
Следовательно,
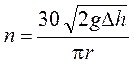 .
.
Максимальное превышение точек с радиусом
R над точкой, лежащей на оси вращения, обозначим ![]() hmax, тогда
hmax, тогда
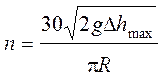 ,
,
где R – радиус сосуда.
3. УРАВНЕНИЕ БЕРНУЛЛИ ДЛЯ ПОТОКА
РЕАЛЬНОЙ ЖИДКОСТИ
Основные уравнения гидродинамики выражают закон сохранения массы и закон сохранения энергии для движущейся жидкости.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.