Гидравлика: Лабораторный практикум, страница 14

Этот график позволил в удобной форме обобщить вопрос о потерях напора на трение и наглядно показать следующее:

-  коэффициент  в общем случае зависит только от Re и D/d;

-  имеются частные случаи движения жидкости, когда  зависит или только от Re, или только от D/d.

На поле графика можно выделить три зоны. Первая зона – зона ламинарного режима: представлена отрезком прямой I. Здесь экспериментальные кривые , найденные для разных D/d, сливаются в одну прямую линию, совпадающую с линией I. Для этой зоны имеем следующее:

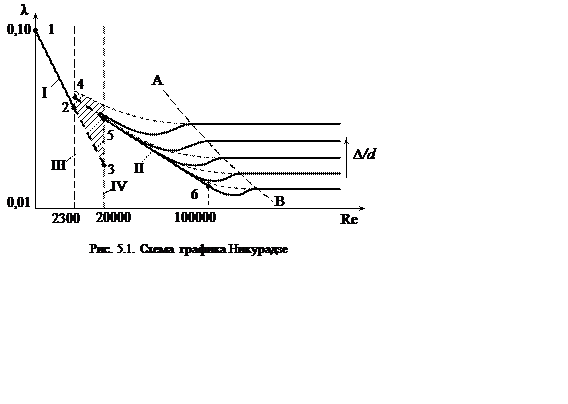-  величины Re малы, Re < 2300;

-  потери на трение  не зависят от шероховатости трубы, а обусловлены лишь трением внутри жидкости;

-  потери напора прямо пропорциональны скорости в первой степени:

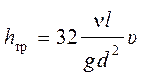,                               (5.5)

где  – кинематический коэффициент вязкости;

 – длина трубопровода.

-  величина l определяется формулой

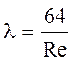.                                      (5.6)

Вторая зона – переходная, расположенная между вертикалями III и IY (зона, внутри которой происходит переход от турбулентного режима к ламинарному и наоборот). В связи со сложным характером движения жидкости в этой области, представить это движение на графике какими-либо определенными кривыми нет возможности. Исключение могут составить только случаи, когда ламинарный режим «затягивается» и имеет место по всей длине трубопровода (рис. 5.1, отрезок 2–3) или когда (в связи с особыми условиями движения) турбулентный режим имеет место по длине всего трубопровода (рис. 5.1, отрезок 4–5).

В этом случае имеют место следующие параметры:

-  числа Рейнольдса лежат в пределах 2300 < Re < 20000;

-  потери напора не зависят от шероховатости трубы, а определяются вязкостью жидкости;

-  коэффициент гидравлического трения вычисляют по зависимости Френкеля

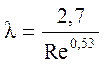.                                 (5.7)

Третья зона – зона турбулентного режима, расположенная правее вертикали IV. При турбулентном течении жидкости в трубах вблизи стенок имеется тонкий пограничный слой с ламинарным режимом движения (рис. 5.2). Толщину этого слоя рассчитывают по зависимости

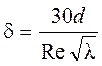.                                 (5.8)

В пределах пограничного слоя скорость по линейному закону нарастает от нулевого значения на стенке до величены скорости основного потока. При увеличении скорости потока, а следовательно, и числа Рейнольдса толщина пограничного слоя dуменьшается (рис.5.3). При большем числе Рейнольдса ламинарный слой практически исчезает. Сопротивление при турбулентном течении жидкости будет зависеть от соотношения толщины пограничного слоя и выступов шероховатости D (рис. 5.1), поэтому зону турбулентного движения можно разбить на три области. Первая область – область гладких труб. Она представлена на графике прямой линией II. В этой области толщина ламинарного слоя больше толщины бугорков шероховатости, последние находятся внутри ламинарного слоя и на сопротивление не влияют (рис. 5.3, а). Трубы в этом случае называются гладкими.

Для области гладких труб характерны следующие параметры:

-  числа Рейнольдса лежат в пределах

20000 < Re < ;

-  потери напора h_тр не зависят от шероховатости, поскольку все кривые D/d = const сливаются в одну линию, совпадающую с линией II (рис.5.1);

-  потери напора, а также l зависят от числа Рейнольдса и могут быть определены по следующим формулам:

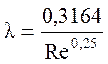,                                     (5.9)

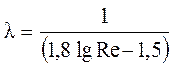;                          (5.10)

-  потери напора пропорциональны скорости в степени 1,75

(h_тр =).

Формула (5.9) называется формулой Блазиуса, а формула (5.10) – формулой Конакова.

Вторая область – область доквадратичного сопротивления шероховатых труб, эта область лежит между прямой II и линией АВ (рис. 5.1). Кривые D/d = const в этой области отклоняются от линии гладких труб II в сторону больших значений l: чем шероховатость меньше, тем при больших числах Рейнольдса начинается это отклонение. По мере увеличения числа Рейнольдса толщина d уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на величину сопротивления (рис. 5.3, б). Стенка в этом случае считается шероховатой.