Таким образом, ламинарное и турбулентное движение представляют два различных вида движения. Они отличаются не только характером движения частиц, но также особенностями распределения скоростей по сечению и видом зависимости между гидравлическим сопротивлением и скоростью.
При течении реальной жидкости возникают силы сопротивления,
обусловленные вязкими напряжениями. Эти силы производят работу, которая целиком
превращается в тепловую энергию. Следовательно, при течении жидкости происходит
процесс необратимого превращения части механической энергии во внутреннюю
энергию. Работа сил вязкости, произведенная между двумя сечениями потока и
отнесенная к единице веса движущейся жидкости, называется потерями напора
![]() . Потери
напора между двумя сечениями потока могут быть определены из уравнения
Бернулли, cоставленного для этих сечений:
. Потери
напора между двумя сечениями потока могут быть определены из уравнения
Бернулли, cоставленного для этих сечений:
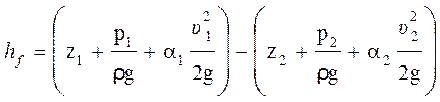 , (5.1)
, (5.1)
где ![]() и
и ![]() – геометрические высоты центров тяжести сечений;
– геометрические высоты центров тяжести сечений; ![]() и
и ![]() – давления в рассматриваемых сечениях;
– давления в рассматриваемых сечениях; ![]() и
и ![]() – средние скорости в сечениях;
– средние скорости в сечениях; ![]() и
и ![]() – коэффициенты неравномерности распределения скоростей в
сечениях; ρ и
– коэффициенты неравномерности распределения скоростей в
сечениях; ρ и ![]() – плотность жидкости и ускорение силы тяжести.
– плотность жидкости и ускорение силы тяжести.
Потери напора при движении жидкости складываются из потерь
напора на трение ![]() и потерь напора на местные сопротивления
и потерь напора на местные сопротивления ![]() :
:
![]() . (5.2)
. (5.2)
Потери напора на трение, или потери по
длине, возникают в чистом виде в прямых трубах постоянного сечения, т. е. при
равномерном течении жидкости. Для горизонтальной трубы постоянного сечения (![]() =
=![]() ,
, ![]() ,
, ![]() ) потери
напора в соответствии с выражением (1) могут быть определены по зависимости
) потери
напора в соответствии с выражением (1) могут быть определены по зависимости
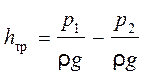 . (5.3)
. (5.3)
Таким образом, при равномерном движении жидкости потери напора по длине трубы определяются разностью пьезометрических высот в сечениях.
Общее выражение для потерь напора на трение при равномерном движении жидкости в трубах, справедливое как для ламинарного, так и для турбулентного режимов, имеет вид
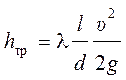 , (5.4)
, (5.4)
где ![]() – коэффициент гидравлического трения.
– коэффициент гидравлического трения.
Эта зависимость называется формулой Дарси-Вейсбаха.
Для грубой количественной оценки шероховатости используется понятие средней высоты выступов. Эта высота, измеряемая в линейных единицах, называется абсолютной шероховатостью и обозначается обычно буквой Δ.
При одной и той же величине абсолютной шероховатости влияние ее на величину гидравлических сопротивлений различно в зависимости от диаметра трубы. Поэтому вводится понятие относительной шероховатости, измеряемой отношением абсолютной шероховатости к диаметру трубы, т. е. Δ/d.
Кроме того, даже при одной и той же абсолютной шероховатости и одинаковом диаметре трубы из разного материала могут иметь совершенно различное сопротивление в зависимости от формы выступов, густоты и характера их расположения и т. д. Учесть это влияние непосредственными измерениями практически невозможно. В связи с этим в практику гидравлических расчетов было введено представление об эквивалентной разнозернистой шероховатости Δэ. Под эквивалентной шероховатостью понимают такую высоту выступов шероховатости, сложенной из песчинок одинакового размера, которая дает одинаковую с заданной шероховатостью величину коэффициента гидравлического трения λ.
При ламинарном движении расчетная зависимость для ![]() может быть
получена чисто теоретическим путем. Ввиду сложности турбулентного течения и
трудности его теоретического исследования до сих пор не создано достаточно
строгой и точной теории этого течения. Поэтому при турбулентном течении
может быть
получена чисто теоретическим путем. Ввиду сложности турбулентного течения и
трудности его теоретического исследования до сих пор не создано достаточно
строгой и точной теории этого течения. Поэтому при турбулентном течении ![]() находится
по различным эмпирическим формулам, предлагаемым разными авторами. Расчетные
формулы для
находится
по различным эмпирическим формулам, предлагаемым разными авторами. Расчетные
формулы для ![]() предусматривают
зависимость этого коэффициента в общем случае только от шероховатости стенок
русла и от числа Рейнольдса. Первые систематические опыты для выявления
характера зависимости
предусматривают
зависимость этого коэффициента в общем случае только от шероховатости стенок
русла и от числа Рейнольдса. Первые систематические опыты для выявления
характера зависимости ![]() от числа Рейнольдса Re и относительной
шероховатости D/d, были проведены Никурадзе в гладких латунных трубах
и трубах с искусственной равнозернистой шероховатостью. Результаты опытов
Никурадзе представил в виде особого графика (рис. 5.1). На нем изображен ряд
кривых, соответствующих различной величине относительной шероховатости D/d, (D – высота выступов
шероховатости, d – диаметр трубы) и две «опорные» прямые: прямая
ламинарного режима I, построенная по уравнению
от числа Рейнольдса Re и относительной
шероховатости D/d, были проведены Никурадзе в гладких латунных трубах
и трубах с искусственной равнозернистой шероховатостью. Результаты опытов
Никурадзе представил в виде особого графика (рис. 5.1). На нем изображен ряд
кривых, соответствующих различной величине относительной шероховатости D/d, (D – высота выступов
шероховатости, d – диаметр трубы) и две «опорные» прямые: прямая
ламинарного режима I, построенная по уравнению 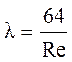 , и прямая II,
построенная по уравнению Блазиуса
, и прямая II,
построенная по уравнению Блазиуса 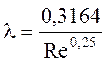 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.