Коллоидная химия: Лабораторный практикум, страница 30

Иногда показания прибора провоцируют запись меньшего числа цифр, чем число досто­верных цифр. Например, если на индикаторе цифро-показывающих весов изображён результат взвешивания 1.000 г, то иногда записывают результат 1 г, имея в виду 1 г точно. В принципе, это не правильно, потому что вводит в заблуждение относительно точности взятой навески : сама по себе (без допонительных пояснений) это запись может быть воспринята как указывающая на то, что истинный результат взвешивания находится где-то между 0.5 и 1.5 г . Поэтому в отчётах о лабораторных измерениях следует соблюдать правило значащих цифр – должны быть записаны все достоверные цифры плюс одна недостоверная цифра.

Вопрос о количестве достоверных цифр, которые показывает калькулятор при вычисле­ниях, является более сложным. Пусть, например, измеренная длина прямоугольника составляет 140 мм, а измеренная ширина – 102 мм. Нас интересует площадь. Результат умножения 140 ´ 102 может быть представлен на индикаторе калькулятора как 14280.00000. Разумеется, не все цифры в этом представлении являются достоверными. Приблизительное правило, которое сле­дует использовать в данном случае, заключается в том, что относительная погрешность вычис­ленного произведения равна сумме относительных погрешностей множителей. Если относитель­ные погрешности измерений длины и ширины составляют 1/140 » 0.007 и 1/102 » 0.009, сумма составляет 0.016. Тогда недостоверность вычисления площади равна 14280 ´ 0.016 » 228 мм², то есть недостоверными являются все цифры, начиная с третьей перед запятой. Поэтому результат вычисления на калькуляторе 14280.00000 следует выписать как 1.43×10⁴ мм², или 143 см², или 1.43 дм². (Но не 14300 мм², потому что в этом числе имеются три недостоверные цифры – тройка и два нуля). Всё это имеет смысл в применении к окончательным результатам вычислений. Если результат вычисления является промежуточным и предназначен для использования в другой фор­муле, то разумно оставить его в памяти калькулятора и затем использовать со всеми недостовер­ными цифрами, то есть в том виде, как он представлен калькулятором.

В других случаях, для оценки числа достоверных цифр в результате вычислений также приходится вычислять абсолютные или относительные погрешности. Пусть требуется вычислить величину y, которая является функцией результатов измерений x₁, x₂, …x_n: y = ¦(x₁, x₂, …x_n). В общем случае абсолютная погрешность Dy и относительная погрешность dy связаны с абсолют­ными погрешностями Dx₁, Dx₂, …Dx_n : 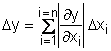                   и 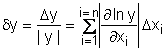                                      (П1.1)

При оценке числа достоверных цифр при вычислениях любой функции следует сначала вычислить величину  y  с высокой точностью, затем вычислить абсолютную погрешность или произведение |y|dy по уравнению П1.1 и округлить вычисленное значение y так, чтобы последняя значащая цифра y отвечала первой значащей цифре абсолютной погрешности.

Поскольку мы не всегда готовы тратить время на подобные вычисления, то часто исполь­зуются более простые, но соответственно менее надёжные правила.

Для действий умножения и деления можно использовать правило наименьшего числа зна­чащих цифр: число значащих цифр произведения или частного должно быть равно наименьшему числу значащих цифр из всех чисел, которыми оперируют при вы­числении.

Для действий сложения и вычитания следует использовать другое правило: результат сложения или вычитания следует округлить до такого числа цифр после разде­лительной запятой, которое является минимальным среди складываемых или вычитаемых чисел.

Эти правила не следует применять слишком формально, поскольку они могут вести к за­вышению или занижению числа достоверных цифр. В частности, если среди чисел, над кото­рыми производятся действия, имеются целые числа, которые не являются результатами измере­ний или округлений, а являются составной частью функции, то их число значащих цифр не должно учитываться. Например, при вычислении диаметр = 2 ´ радиус, число значащих цифр результата должно отвечать числу значащих цифр величины радиуса, но не числу значащих цифр коэффициента 2.